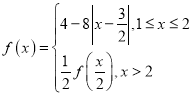题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的极大值点;
的极大值点;
(2)若函数![]() ,判断
,判断![]() 的单调性;
的单调性;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)求导![]() ,求出
,求出![]() 的单调区间后即可得解;
的单调区间后即可得解;
(2)由题意得![]() ,根据
,根据![]() 、
、![]() 、
、![]() 、
、![]() 分类讨论
分类讨论![]() 的正负,即可得解;
的正负,即可得解;
(3)由![]() 可得
可得![]() ,
,![]() 且
且![]() ,则可得
,则可得![]() ,
,![]() ,令
,令![]() ,根据
,根据![]() 的单调性求出
的单调性求出![]() 的最大值后即可得解.
的最大值后即可得解.
(1)当![]() 时,
时,![]() .当
.当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减.所以
单调递减.所以![]() 是
是![]() 的极大值点.
的极大值点.
(2)由已知得![]() ,
,
![]() 的定义域为
的定义域为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() .
.
因而当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() .
.
因而当![]() 与
与![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
当![]() 时,
时,![]() ,因而当
,因而当![]() 时,
时,![]() 单调递增.
单调递增.
当![]() 时,由
时,由![]() .得
.得![]() 或
或![]() ,
,
因而当![]() 与
与![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 与
与![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)![]() ,则
,则![]() 的定义域为
的定义域为![]() .
. ![]() .
.
若![]() 有两个极值点
有两个极值点![]() ,则方程
,则方程![]() 的判别式
的判别式![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
又![]() ,∴
,∴![]() 即
即![]() .
.

![]() ,
,
设![]() 其中
其中![]() .
.
由![]() 得
得![]() .
.
由于![]() 即
即![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
即![]() 的最大值为
的最大值为![]() .
.
从而![]() 成立.
成立.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: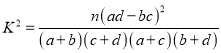
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |