题目内容
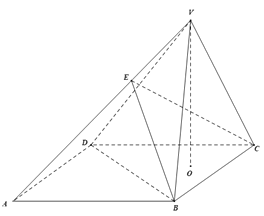
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 为正方形
为正方形![]() 内一点,它到边
内一点,它到边![]() ,
,![]() 的距离分别是1,2,
的距离分别是1,2,![]() 平面
平面![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,
,
(1)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据题意,如下图,建立空间直角坐标系,分别求出![]() 和
和![]() ,,再利用向量法,根据异面直线夹角公式求出即可;
,,再利用向量法,根据异面直线夹角公式求出即可;
(2)根据向量共线![]() ,求出点
,求出点![]() 坐标,分别求出平面
坐标,分别求出平面![]() 和平面
和平面![]() 的的法向量,再利用向量的二面角公式求出结果.
的的法向量,再利用向量的二面角公式求出结果.
(1)如图,过![]() 作
作![]() 的垂线为
的垂线为![]() 轴,
轴,
作![]() 的垂线为
的垂线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
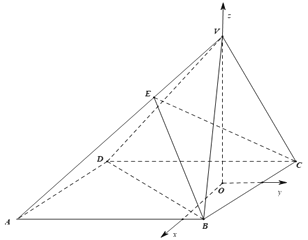
建立直角坐标系,则
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
∴![]() ,
,![]() ,
,
设直线![]() 与
与![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
∴直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() .
.
(2)设![]() ,由
,由![]() ,即
,即![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,
,
则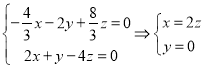 ,取
,取![]() ,∴
,∴![]() ,
,
![]()
![]() ,
,![]() ,设面
,设面![]() 的法向量为
的法向量为![]() ,
,
则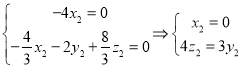 ,取
,取![]() ,则
,则![]() ,∴
,∴![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: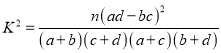
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?