题目内容
13.如图,梯形ABCD中,AD∥BC,AD:BC=a:b,中位线EF=m,则图示MN的长是( )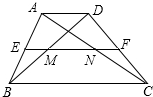
| A. | $\frac{m(a+b)}{a-b}$ | B. | $\frac{m(a-b)}{a+b}$ | C. | $\frac{m(a-b)}{2(a+b)}$ | D. | $\frac{m(b-a)}{a+b}$ |
分析 先由梯形中位线定理,得出EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC),又EF分别交AC、BD于点N、M,得到M、N分别为BD、AC中点,根据三角形中位线定理得出EM=$\frac{1}{2}$AD,FN=$\frac{1}{2}$AD,MN=EF-EM-FN=$\frac{1}{2}$(BC-AD),根据AD:BC=a:b,中位线EF=m,EF=$\frac{1}{2}$(AD+BC),即可求出MN.
解答 解:∵EF为梯形ABCD的中位线,
∴EF∥AD∥BC,EF=$\frac{1}{2}$(AD+BC),
∵EF分别交AC、BD于点N、M,
∴M、N分别为BD、AC中点,
∴EM、FN分别是△ABD、△ACD的中位线,
∴EM=$\frac{1}{2}$AD,FN=$\frac{1}{2}$AD,
∴MN=EF-EM-FN=$\frac{1}{2}$(BC-AD),
∵AD:BC=a:b,中位线EF=m,EF=$\frac{1}{2}$(AD+BC),
∴BC=$\frac{2mb}{a+b}$,AD=$\frac{2ma}{a+b}$,
∴MN=$\frac{m(a-b)}{a+b}$,
故选:D.
点评 本题考查了梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.同时考查了三角形中位线定理.

练习册系列答案
相关题目
4.某问学在5次数学测试中的成绩如表所示,在这个函数中,定义域是{1,2,3,4,5},值域是{85,86,88,93,95}.
| 次 数 | 1 | 2 | 3 | 4 | 5 |
| 分 数 | 85 | 88 | 93 | 86 | 95 |
5.已知1-x+x2-x3+…+x8=a0+a1(x+1)+a2(x+1)2+…+a8(x+1)8.则a2=( )
| A. | 120 | B. | 56 | C. | 72 | D. | 84 |
2.在区间[0,1]内随机取1个数记为a,则使得函数f(x)=x2+x+a有零点的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |