题目内容
5.若$\overrightarrow{a}$=(sin2x,1),$\overrightarrow{b}$=(1,-cos2x),设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(1)求函数y=f(x)的最小正周期;
(2)求函数y=f(x)的单调增区间.
分析 (1)由平面向量数量积的运算及三角函数中的恒等变换应用可得函数解析式f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),利用周期公式即可得解.
(2)由2k$π-\frac{π}{2}$≤2x-$\frac{π}{4}$$≤2kπ+\frac{π}{2}$,k∈Z可解得函数y=f(x)的单调增区间.
解答 解:(1)∵f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∴函数y=f(x)的最小正周期T=$\frac{2π}{2}=π$;
(2)由2k$π-\frac{π}{2}$≤2x-$\frac{π}{4}$$≤2kπ+\frac{π}{2}$,k∈Z可解得函数y=f(x)的单调增区间为:[k$π-\frac{π}{8}$,k$π+\frac{3π}{8}$],k∈Z.
点评 本题主要考查了三角函数中的恒等变换应用,平面向量数量积的运算,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
13.如图,梯形ABCD中,AD∥BC,AD:BC=a:b,中位线EF=m,则图示MN的长是( )
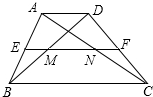

| A. | $\frac{m(a+b)}{a-b}$ | B. | $\frac{m(a-b)}{a+b}$ | C. | $\frac{m(a-b)}{2(a+b)}$ | D. | $\frac{m(b-a)}{a+b}$ |
20.方程y2=x表示同一条曲线的参数方程(t为参数)的是( )
| A. | $\left\{\begin{array}{l}{x=si{n}^{2}t}\\{y=sint}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=t}\\{y={t}^{2}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=\frac{1-cos2t}{1+cos2t}}\\{y=tant}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=t}\\{y=\sqrt{|t|}}\end{array}\right.$ |
14.数列{an}中,an=n2-9n-100,则最小的项是( )
| A. | 第4项 | B. | 第5项 | C. | 第6项 | D. | 第4项或第5项 |
15.把语文、数学、物理三本书随机地分给甲、乙、丙三位同学.每人一本,则事件“甲同学分得语文书”与事件“乙同学分得语文书”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上答案都不对 |