题目内容
3.用三角函数诱导公式求值:sin(-$\frac{31π}{6}$)-cos(-$\frac{10π}{3}$)-sin$\frac{11π}{10}$.分析 原式利用正弦、余弦函数的奇偶性化简,角度变形后利用诱导公式及特殊角的三角函数值计算即可得到结果.
解答 解:原式=-sin(5π+$\frac{π}{6}$)-cos(3π+$\frac{π}{3}$)-sin(π+$\frac{π}{10}$)
=sin$\frac{π}{6}$+cos$\frac{π}{3}$+sin$\frac{π}{10}$
=$\frac{1}{2}$+$\frac{1}{2}$+sin$\frac{π}{10}$
=1+sin$\frac{π}{10}$.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.如图,梯形ABCD中,AD∥BC,AD:BC=a:b,中位线EF=m,则图示MN的长是( )
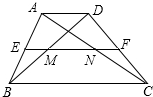

| A. | $\frac{m(a+b)}{a-b}$ | B. | $\frac{m(a-b)}{a+b}$ | C. | $\frac{m(a-b)}{2(a+b)}$ | D. | $\frac{m(b-a)}{a+b}$ |
14.数列{an}中,an=n2-9n-100,则最小的项是( )
| A. | 第4项 | B. | 第5项 | C. | 第6项 | D. | 第4项或第5项 |
15.把语文、数学、物理三本书随机地分给甲、乙、丙三位同学.每人一本,则事件“甲同学分得语文书”与事件“乙同学分得语文书”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上答案都不对 |
13.如图是一个算法的程序框图,若输入的x的值为2,则输出的y的值是( )
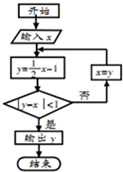

| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -$\frac{7}{4}$ |