题目内容
2.在区间[0,1]内随机取1个数记为a,则使得函数f(x)=x2+x+a有零点的概率为( )| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 由函数f(x)=x2+x+a有零点,利用根的判别式求出a的取值范围,由此利用几何概型能求出使得函数f(x)=x2+x+a有零点的概率.
解答 解:∵函数f(x)=x2+x+a有零点,
∴△=1-4a≥0,解得a$≤\frac{1}{4}$,
∵a∈[0,1],∴0≤a≤$\frac{1}{4}$,
∴使得函数f(x)=x2+x+a有零点的概率为:
p=$\frac{\frac{1}{4}-0}{1-0}$=$\frac{1}{4}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要注意根的判别式和几何概型的合理运用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
13.如图,梯形ABCD中,AD∥BC,AD:BC=a:b,中位线EF=m,则图示MN的长是( )
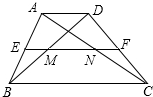

| A. | $\frac{m(a+b)}{a-b}$ | B. | $\frac{m(a-b)}{a+b}$ | C. | $\frac{m(a-b)}{2(a+b)}$ | D. | $\frac{m(b-a)}{a+b}$ |
14.数列{an}中,an=n2-9n-100,则最小的项是( )
| A. | 第4项 | B. | 第5项 | C. | 第6项 | D. | 第4项或第5项 |