题目内容
18.如图,已知$\overrightarrow{AD}$=4$\overrightarrow{AB}$,$\overrightarrow{DE}$=4$\overrightarrow{BC}$,试判断$\overrightarrow{AC}$与$\overrightarrow{AE}$是否共线.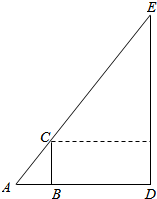
分析 根据平面向量的线性运算,利用平面向量的共线定理,即可判断$\overrightarrow{AC}$与$\overrightarrow{AE}$是否共线.
解答 解:∵$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$,
且$\overrightarrow{AD}$=4$\overrightarrow{AB}$,$\overrightarrow{DE}$=4$\overrightarrow{BC}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=4$\overrightarrow{AB}$+4$\overrightarrow{BC}$=4($\overrightarrow{AB}$+$\overrightarrow{BC}$)=4$\overrightarrow{AC}$,
∴$\overrightarrow{AC}$与$\overrightarrow{AE}$共线.
点评 本题考查了平面向量的线性运算问题,也考查了平面向量共线定理的应用问题,是基础题目.

练习册系列答案
相关题目
13.如图,梯形ABCD中,AD∥BC,AD:BC=a:b,中位线EF=m,则图示MN的长是( )
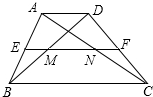

| A. | $\frac{m(a+b)}{a-b}$ | B. | $\frac{m(a-b)}{a+b}$ | C. | $\frac{m(a-b)}{2(a+b)}$ | D. | $\frac{m(b-a)}{a+b}$ |