题目内容
3.对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[-1.08]=-2,定义函数f(x)=x-[x],给定下列叙述:①函数f(x)的最大值为1;②函数f(x)的最小值为0;③函数G(x)=f(x)-$\frac{1}{2}$有无数个零点;④函数f(x)是增函数.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 定义函数f(x)=x-[x],其图象:f(x)=$\left\{\begin{array}{l}{0,当x为整数时}\\{(0,1),当x不为整数时}\end{array}\right.$. 即可得出.
解答 解:定义函数f(x)=x-[x],其图象: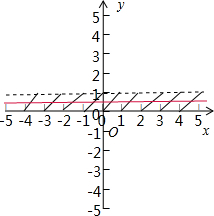
∴f(x)=$\left\{\begin{array}{l}{0,当x为整数时}\\{(0,1),当x不为整数时}\end{array}\right.$.
可得:①函数f(x)的最大值为1,不正确;
②函数f(x)的最小值为0,正确;
③函数G(x)=f(x)-$\frac{1}{2}$有无数个零点,正确;
④函数f(x)是周期函数,不是增函数,因此不正确.
其中正确的个数为2.
故选:B.
点评 本题考查了取整函数[x]的图象与性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
13.θ∈[0,π],$cosθ=\frac{3}{4}$,则$tan\frac{θ}{2}$=( )
| A. | $\sqrt{7}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
14.抛物线$y=\frac{1}{8}{x^2}$的焦点到双曲线${y^2}-\frac{x^2}{3}=1$的一条渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
15.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,以下说法正确的是( )
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
13.已知实数x、y、z满足x2+y2+z2=4,则(2x-y)2+(2y-z)2+(2z-x)2的最大值是( )
| A. | 12 | B. | 20 | C. | 28 | D. | 36 |
 如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB. 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.