题目内容
12. 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.(1)求证:DE是圆O的切线;
(2)若∠CAB=60°,⊙O的半径为2,EC=1,求DE的值.
分析 (1)连接OD,由已知得∠ODA=∠OAD=∠DAC,从而OD∥AE,由此能证明DE是圆O的切线.
(2)连结BC,由已知得AC=2,AE=EC+CA=3,由此利用圆的切割线定理能求出DE的值.
解答 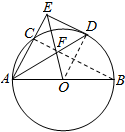 (1)证明:连接OD,
(1)证明:连接OD,
∵AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,
∴∠ODA=∠OAD=∠DAC,∴OD∥AE,…(3分)
又AE⊥DE,∴DE⊥OD,又OD为半径,
∴DE是圆O的切线.…(5分)
(2)解:连结BC,在Rt△ABC中,∠CAB=60°,AB=4,
∴AC=ABcos60°=2…(7分)
又∵EC=1,∴AE=EC+CA=3,
由圆的切割线定理得:
DE2=CE•EA=3,∴$DE=\sqrt{3}$.…(10分)
点评 本题考查圆的切线的证明,考查线段长的求法,是中档题,解题时要认真审题,注意圆的切割线定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知函数f(x)=x2-2x+3,当0≤x≤m时,该函数有最大值3,最小值2,则实数m的取值范围是( )
| A. | [1,+∞) | B. | [0,2] | C. | (-∞,2] | D. | [1,2] |
1.执行如图所示的程序框图,则输出i的值为( )
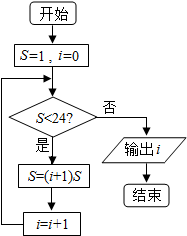

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
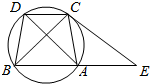 如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.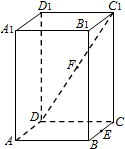 在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: