题目内容
13.θ∈[0,π],$cosθ=\frac{3}{4}$,则$tan\frac{θ}{2}$=( )| A. | $\sqrt{7}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
分析 由条件利用二倍角公式求得cos$\frac{θ}{2}$ 和sin$\frac{θ}{2}$的值,再利用同角三角函数的基本关系式求得$tan\frac{θ}{2}$的值.
解答 解:∵${cos^2}\frac{θ}{2}=\frac{1+cosθ}{2}=\frac{7}{8}$,又$\frac{θ}{2}∈[0,\frac{π}{2}]$,∴$cos\frac{θ}{2}=\frac{{\sqrt{14}}}{4}$,∴所以,$sin\frac{θ}{2}=\sqrt{1-{{cos}^2}\frac{θ}{2}}=\frac{{\sqrt{2}}}{4}$,∴$tan\frac{θ}{2}=\frac{{sin\frac{θ}{2}}}{{cos\frac{θ}{2}}}=\frac{{\sqrt{7}}}{7}$,
故选:B.
点评 本题主要考查二倍角公式、同角三角函数的基本关系式,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
8.已知复数 $z=\frac{1-i}{i}$的共轭复数为( )
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
18.已知球面上有A、B、C三点,BC=2$\sqrt{3}$,AB=AC=2,若球的表面积为20π,则球心到平面ABC的距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.已知A(1,5),B(5,-2),在x轴上存在一点M,使|MA|=|MB|,则点M的坐标为( )
| A. | $(\frac{8}{3},0)$ | B. | $(\frac{3}{8},0)$ | C. | $(-\frac{8}{3},0)$ | D. | $(-\frac{3}{8},0)$ |
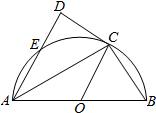 如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )
如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )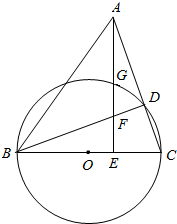 如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.
如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.