题目内容
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
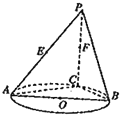
【答案】(1)l∥平面PAC,见解析 (2)见解析
【解析】
(1)直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,所以EF∥AC,
又EF平面ABC,且AC平面ABC,所以EF∥平面ABC.
而EF平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l平面PAC,EF平面PAC,所以直线l∥平面PAC.
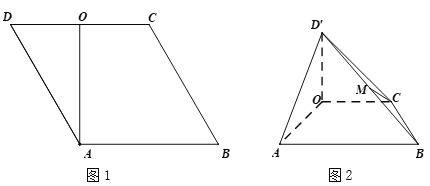
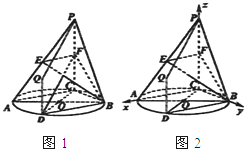
(2)(综合法)如图1,连接BD,由(1)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF平面PBC,所以l⊥BF.
故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.
由![]() ,作DQ∥CP,且
,作DQ∥CP,且![]() .
.
连接PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得![]() ,
,
从而![]() .
.
(2)(向量法)如图2,由![]() ,作DQ∥CP,且
,作DQ∥CP,且![]() .
.
连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量![]() 所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
设CA=a,CB=b,CP=2c,则有
![]() .
.
于是![]() ,
,
∴![]() =
=![]() ,从而
,从而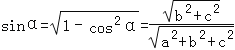 ,
,
又取平面ABC的一个法向量为![]() ,可得
,可得![]() ,
,
设平面BEF的一个法向量为![]() ,
,
所以由![]() 可得
可得 .
.
于是![]() ,从而
,从而![]() .
.
故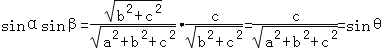 ,即sinθ=sinαsinβ.
,即sinθ=sinαsinβ.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
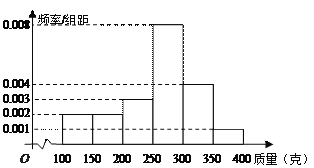
启东小题作业本系列答案【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本3元,且以8元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计,得到如下需求量表。该蛋糕店一天制作了这款蛋糕![]() 个,以
个,以![]() (单位:个,
(单位:个,![]() ,
,![]() )表示当天的市场需求量,
)表示当天的市场需求量,![]() (单位:元)表示当天出售这款蛋糕获得的利润.
(单位:元)表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
,![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于570元的天数中,按需求量分层抽样抽取6天.
不少于570元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润![]() 关于市场需求量
关于市场需求量![]() 的函数解析式,并求这6天中利润为650元的天数;
的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.