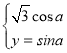题目内容
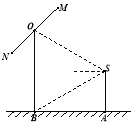
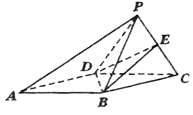
【题目】如图所示,在四棱锥P-ABCD中,四边形ABCD为平行四边形,△PCD为正三角形,∠BAD=30°,AD=4,AB=2![]() ,平面PCD⊥平面ABCD,E为PC中点.
,平面PCD⊥平面ABCD,E为PC中点.
(1)证明:BE⊥PC;
(2)求多面体PABED的体积.
【答案】(1)见解析;(2)3![]()
【解析】
(1)先证明PC⊥面BDE,再证明BE⊥PC;
(2)先求![]() 的体积,再求
的体积,再求![]() 的体积,从而可得多面体PABED的体积.
的体积,从而可得多面体PABED的体积.
(1)∵BD2=AB2+AD2![]() 2ABADcos∠BAD=4,∴BD=2,
2ABADcos∠BAD=4,∴BD=2,
∴∠ABD=90°,∴BD⊥CD,∵面PCD⊥面ABCD,面PCD∩面ABCD=CD,
∴BD⊥面PCD,∴BD⊥PC,∵△PCD是正三角形,E为PC的中点,∴DE⊥PC,
∴PC⊥面BDE,∴BE⊥PC.
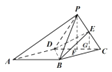
(2)作PF⊥CD,EG⊥CD,F,G为垂足,∵面PCD⊥面ABCD,
∴PF⊥面ABCD,EG⊥面ABCD,∵△PCD是正三角形,CD=2![]() ,
,
∴PF=3,EG=![]() ,∴VP-ABCD=
,∴VP-ABCD=![]() =4
=4![]() ,
,
![]() =
=![]() ,
,
∴多面体PABED的体积V=VP-ABCD-VE-BCD=4![]() =3
=3![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3 000人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 | |||
调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 500人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(1)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.