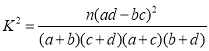题目内容
【题目】如图,三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
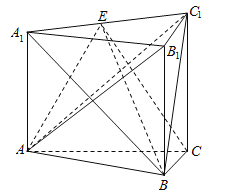
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)设平面![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长
的长
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(Ⅰ)证明![]() 平面
平面![]() .推出
.推出![]() .然后证明
.然后证明![]() 平面
平面![]() .得到
.得到![]() .
.![]() .即可证明
.即可证明![]() 平面
平面![]() .
.
(Ⅱ)说明![]() .证明
.证明![]() 平面
平面![]() .通过
.通过![]() 求解即可.
求解即可.
(Ⅲ)证明![]() .说明
.说明![]() 为
为![]() 中点.然后求解即可.
中点.然后求解即可.
解:(Ⅰ)因为三棱柱![]() 中,
中,
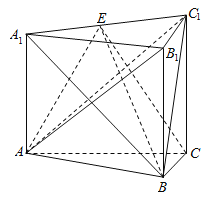
侧棱垂直于底面,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 为菱形.
为菱形.
所以![]() .
.
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)由已知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() ,故
,故![]() 到平面
到平面![]() 的距离为2.
的距离为2.
因为![]() 为
为![]() 中点,所以
中点,所以![]() 点到平面
点到平面![]() 距离为1.
距离为1.
所以![]()
(Ⅲ)在三棱柱![]() 中,
中,

因为![]() ,
,![]() 为平面
为平面![]() 与平面
与平面![]() 的公共点,
的公共点,
所以平面![]() 平面
平面![]() .
.
因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点.
中点.
所以![]()

练习册系列答案
相关题目
【题目】已知某商品每件的生产成本![]() (元)与销售价格
(元)与销售价格![]() (元)具有线性相关关系,对应数据如表所示:
(元)具有线性相关关系,对应数据如表所示:
| 5 | 6 | 7 | 8 |
| 15 | 17 | 21 | 27 |
(1)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该商品的月销售量![]() (千件)与生产成本
(千件)与生产成本![]() (元)的关系为
(元)的关系为![]() ,
,![]() ,根据(1)中求出的线性回归方程,预测当
,根据(1)中求出的线性回归方程,预测当![]() 为何值时,该商品的月销售额最大.
为何值时,该商品的月销售额最大.
附: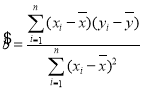 ,
,![]() .
.