题目内容
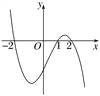
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )
A. 函数f(x)有极大值f(2)和极小值f(1) B. 函数f(x)有极大值f(-2)和极小值f(1)
C. 函数f(x)有极大值f(2)和极小值f(-2) D. 函数f(x)有极大值f(-2)和极小值f(2)
【答案】D
【解析】试题分析:利用函数的图象,判断导函数值为0时,左右两侧的导数的符号,即可判断极值.
解:由函数的图象可知,f′(﹣2)=0,f′(2)=0,并且当x<﹣2时,f′(x)>0,当﹣2<x<1,f′(x)<0,函数f(x)有极大值f(﹣2).
又当1<x<2时,f′(x)<0,当x>2时,f′(x)>0,故函数f(x)有极小值f(2).
故选D.

练习册系列答案
相关题目