题目内容
【题目】已知函数f(x)=ax+x2,g(x)=xlna,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=![]() -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
【答案】(1)见解析(2)(2-![]() ,0)∪(2+
,0)∪(2+![]() ,+∞)(3)(1,e2]
,+∞)(3)(1,e2]
【解析】
(1)∵F(x)=f(x)-g(x)=ax+x2-xlna,
∴F′(x)=ax·lna+2x-lna=(ax-1)lna+2x.
∵a>1,x>0,∴ax-1>0,lna>0,2x>0,
∴当x∈(0,+∞)时,F′(x)>0,即函数F(x)在区间(0,+∞)上单调递增.
(2)由(1)知当x∈(-∞,0)时,F′(x)<0,
∴F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.
∴F(x)的最小值为F(0)=1.由![]() -3=0,
-3=0,
得F(x)=b-![]() +3或F(x)=b-
+3或F(x)=b-![]() -3,
-3,
∴要使函数y=![]() -3有四个零点,只需
-3有四个零点,只需
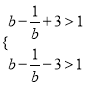 即b-
即b-![]() >4,即
>4,即![]() >0,
>0,
解得b>2+![]() 或2-
或2-![]() <b<0.
<b<0.
故b的取值范围是(2-![]() ,0)∪(2+
,0)∪(2+![]() ,+∞).
,+∞).
(3)∵x1,x2∈[-1,1],由(1)知F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴F(x)min=F(0)=1.
从而再来比较F(-1)与F(1)的大小即可.
F(-1)=![]() +1+lna
+1+lna
∴F(1)-F(-1)=a-![]() -2lna.
-2lna.
令H(x)=x-![]() -2lnx(x>0),
-2lnx(x>0),
则H′(x)=1+![]() -
-![]() =
=![]() =
=![]() >0,
>0,
∴H(x)在(0,+∞)上单调递增.
∵a>1,∴H(a)>H(1)=0.∴F(1)>F(-1).
∴|F(x2)-F(x1)|的最大值为|F(1)-F(0)|=a-lna,
∴要使|F(x2)-F(x1)|≤e2-2恒成立,只需a-lna≤e2-2即可.令h(a)=a-lna(a>1),h′(a)=1-![]() >0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]
>0,∴h(a)在(1,+∞)上单调递增.∵h(e2)=e2-2,∴只需h(a)≤h(e2),即1<a≤e2.故a的取值范围是(1,e2]

 阅读快车系列答案
阅读快车系列答案