题目内容
已知m为常数,函数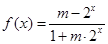 为奇函数.
为奇函数.
(1)求m的值;
(2)若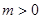 ,试判断
,试判断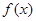 的单调性(不需证明);
的单调性(不需证明);
(3)若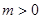 ,存在
,存在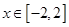 ,使
,使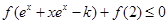 ,求实数k的最大值.
,求实数k的最大值.
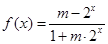 为奇函数.
为奇函数.(1)求m的值;
(2)若
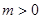 ,试判断
,试判断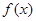 的单调性(不需证明);
的单调性(不需证明);(3)若
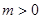 ,存在
,存在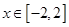 ,使
,使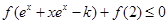 ,求实数k的最大值.
,求实数k的最大值.(1)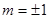 ;(2)在R上单调递增;(3)
;(2)在R上单调递增;(3)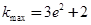 .
.
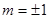 ;(2)在R上单调递增;(3)
;(2)在R上单调递增;(3)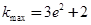 .
.试题分析: (1)由奇函数的定义得:
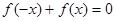 ,将解析式代入化简便可得m的值;
,将解析式代入化简便可得m的值;(2)
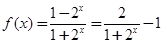 ,结合指数函数与反比例函数的单调性,便可判定
,结合指数函数与反比例函数的单调性,便可判定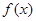 的单调性;
的单调性;(3)对不等式:
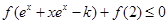 ,不宜代入解析式来化简,而应将进行如下变形:
,不宜代入解析式来化简,而应将进行如下变形: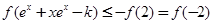 ,然后利用单调性去掉
,然后利用单调性去掉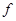 ,从而转化为:
,从而转化为: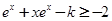 .
.进而变为:
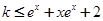 .由题设知:
.由题设知: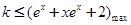 .这样只需求出
.这样只需求出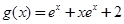 的最大值即可. 而
的最大值即可. 而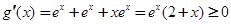 ,所以
,所以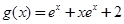 在[-2,2]上单调递增,
在[-2,2]上单调递增,所以
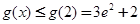 .
.试题解析:(1)由
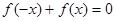 ,得
,得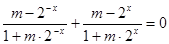 ,
,∴
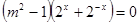 ,即
,即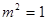 ,
,∴
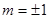 . ..4分
. ..4分(2)
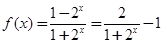 ,在R上单调递增. 7分
,在R上单调递增. 7分(3)由
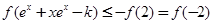 得
得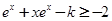 ,9分
,9分即
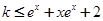 .
.令
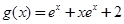 ,则
,则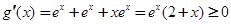 ,
,所以
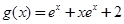 在[-2,2]上单调递增,
在[-2,2]上单调递增,所以
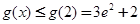 ,
,所以
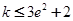 ,从而
,从而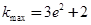 .12分
.12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
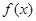 是定义在
是定义在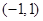 上的奇函数,且
上的奇函数,且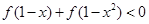 .
.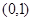 上是减函数的是( )
上是减函数的是( )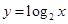
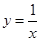
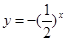
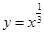
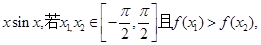 则下列结论正确的是( )
则下列结论正确的是( )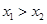
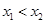

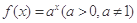 在
在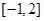 上的最大值为4,最小值为m,且函数
上的最大值为4,最小值为m,且函数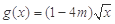 在
在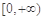 上是增函数,则a=( )
上是增函数,则a=( )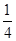

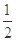
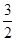
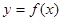 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当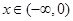 时
时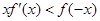 成立(其中
成立(其中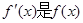 的导函数),若
的导函数),若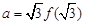 ,
,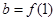 ,
,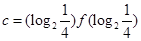 则
则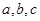 的大小关系是( )
的大小关系是( ) 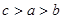
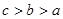

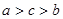
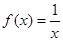
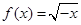
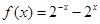
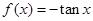
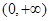 上递增的函数为( )
上递增的函数为( )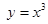
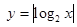
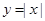
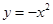
 )
)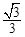 )
)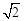 )
) )
)