题目内容
如图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )


| A.是45° | B.是60° |
| C.是90° | D.随P点的移动而变化 |
C
试题分析:画出图形,利用长方体的性质,三垂线定理推出BP⊥B1C,得到选项.解:∵D1C1⊥面BCC1B1,
∴BC1为BP在面BCC1B1内的射影,又BC1=B1C,∴BC1⊥B1C,∴BP⊥B1C.异面直线PB与B1C所成角的大小90°.故选C.
点评:本题主要考查长方体的性质和求异面直线所成角的求法,三垂线定理的应用,考查空间想象能力,计算能力

练习册系列答案
相关题目
 ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
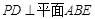 ;
; 的平面角的正弦值.
的平面角的正弦值. -
- ,
, =2,
=2,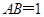 ,
, ,
, 分别在
分别在 ,
,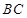 上移动,且始终保持
上移动,且始终保持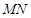 ∥平面
∥平面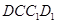 ,设
,设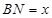 ,
,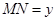 ,则函数
,则函数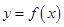 的图象大致是( )
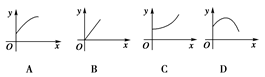
的图象大致是( )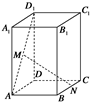
 a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l
a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l 的棱长为1,点
的棱长为1,点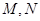 分别是
分别是 和
和 的中点
的中点

 与
与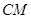 所成角的余弦值。
所成角的余弦值。 M,b
M,b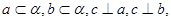 则
则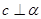 ;②。若
;②。若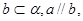 则
则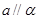 ;
;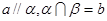 ,则
,则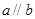 ; ④。若
; ④。若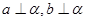 ,则
,则 是空间三条不同的直线,
是空间三条不同的直线, 是空间中不同的平面,则下列命题中不正确的是( )
是空间中不同的平面,则下列命题中不正确的是( ) ,
, ,则
,则
 ,
, ,则
,则
 且
且 是
是 在
在 内的射影,若
内的射影,若 ,则
,则
 时,若
时,若 ,则
,则
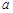 、
、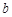 是不同的两条直线,
是不同的两条直线,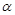 、
、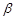 是不同的两个平面,分析下列命题,其中正确的是( ).
是不同的两个平面,分析下列命题,其中正确的是( ).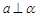 ,
, ,
,

 ,
,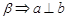
 ,
,