题目内容
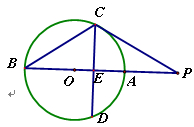
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.
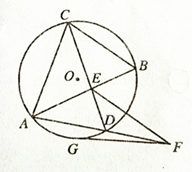
求证:(1)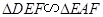 ;(2)EF//CB.
;(2)EF//CB.

求证:(1)
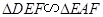 ;(2)EF//CB.
;(2)EF//CB.(1)证明过程详见解析(2)证明过程详见解析
试题分析:本题考查切割线定理、三角形相似、同弧所对的圆周角相等、同位角相等等基础知识,考查学生的逻辑推理能力、转化能力.第一问,利用切割线定理得到FG2=FA·FD,利用已知的等量关系代换式子中的FG,即得到△FED与△EAF中边的比例关系,再由于2个三角形有一个公共角,所以得到2个三角形相似;第二问,由第一问的相似得∠FED=∠FAE,利用同弧所对的圆周角相等得∠FAE=∠DAB=∠DCB,即∠FED=∠BCD,利用同位角相等得EF∥CB.
试题解析:(1)由切割线定理得FG2=FA·FD.
又EF=FG,所以EF2=FA·FD,即
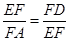 .
.因为∠EFA=∠DFE,所以△FED∽△EAF. 6分
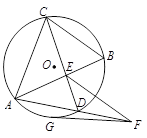
(2)由(1)得∠FED=∠FAE.
因为∠FAE=∠DAB=∠DCB,
所以∠FED=∠BCD,所以EF∥CB. 10分

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
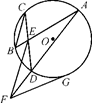

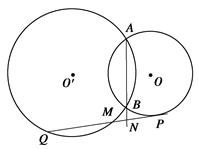
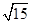
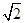
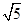
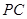 与圆
与圆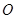 相切于
相切于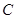 ,割线
,割线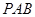 经过圆心
经过圆心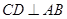 于点
于点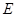 ,
,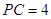 ,
,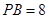 ,则
,则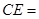 ___.
___.
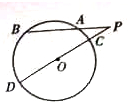
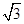 ,若∠CAP=30°,则PB= .
,若∠CAP=30°,则PB= . 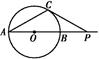
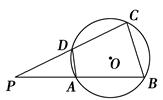
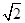 ,求AF的长.
,求AF的长.