题目内容
已知a、b为实数,且b>a>e,其中e为自然对数的底,
求证: ab>ba.
求证: ab>ba.
证明略
证法一: ∵b>a>e,∴要证ab>ba,只要证blna>alnb,
设f(b)=blna-alnb(b>e),则f′(b)=lna-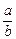 .
.
∵b>a>e,∴lna>1,且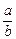 <1,∴f′(b)>0.
<1,∴f′(b)>0.
∴函数f(b)=blna-alnb在(e,+∞)上是增函数,
∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,
∴blna>alnb,∴ab>ba.
证法二: 要证ab>ba,只要证blna>alnb(e<a<b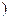 ,即证
,即证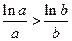 ,
,
设f(x)=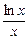 (x>e),则f′(x)=
(x>e),则f′(x)=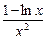 <0,
<0,
∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即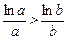 ,∴ab>ba.
,∴ab>ba.
设f(b)=blna-alnb(b>e),则f′(b)=lna-
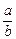 .
.∵b>a>e,∴lna>1,且
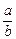 <1,∴f′(b)>0.
<1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,
∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,
∴blna>alnb,∴ab>ba.
证法二: 要证ab>ba,只要证blna>alnb(e<a<b
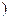 ,即证
,即证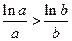 ,
,设f(x)=
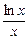 (x>e),则f′(x)=
(x>e),则f′(x)=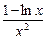 <0,
<0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即
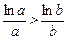 ,∴ab>ba.
,∴ab>ba.
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (b、c为常数).
(b、c为常数).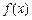 在
在
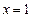 和
和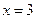 处取得极值,试求
处取得极值,试求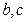 的值;
的值;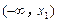 、
、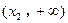 上单调递增,且在
上单调递增,且在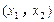 上单调递减,又满足
上单调递减,又满足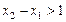 ,求证:
,求证: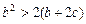 。
。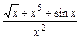 ;
;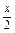 (1-2cos2
(1-2cos2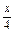 );
);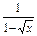 +
+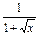 .
.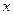 的三次函数
的三次函数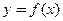 的两个极值点为P、Q,其中P为原点,Q在曲线
的两个极值点为P、Q,其中P为原点,Q在曲线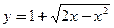 上,则曲线
上,则曲线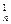 +2C
+2C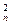 +3C
+3C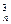 +…+nC
+…+nC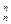 ,(n∈N*)
,(n∈N*)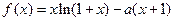 ,其中
,其中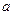 为常数.
为常数.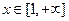 时,
时,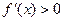 恒成立,求
恒成立,求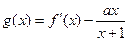 的单调区间.
的单调区间.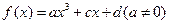 是
是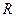 上的奇函数,当
上的奇函数,当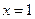 时
时 取得极值
取得极值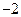 .
.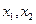
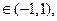 不等式
不等式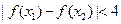 恒成立.
恒成立.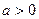 ,函数
,函数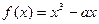 ,在
,在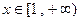 是一个单调函数。
是一个单调函数。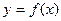 在
在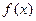 在
在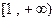 上是单调递增函数,求实数a的取值范围。
上是单调递增函数,求实数a的取值范围。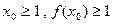 且
且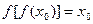 ,比较
,比较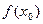 与
与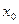 的大小。
的大小。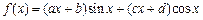 ,试确定常数
,试确定常数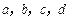 ,使得
,使得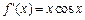 .
.