题目内容
(本小题满分15分)已知数列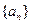 中,
中,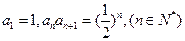 .
.
???(Ⅰ)求证:数列 (
(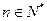 )均为等比数列;??(Ⅱ)求数列
)均为等比数列;??(Ⅱ)求数列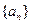 的前
的前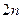 项和
项和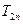 ;???(Ⅲ)若数列
;???(Ⅲ)若数列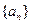 的前
的前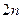 项和为
项和为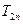 ,不等式
,不等式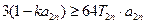 对
对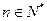 恒成立,求
恒成立,求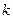 的最大值.
的最大值.
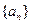 中,
中,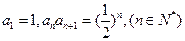 .
.???(Ⅰ)求证:数列
 (
(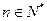 )均为等比数列;??(Ⅱ)求数列
)均为等比数列;??(Ⅱ)求数列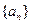 的前
的前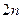 项和
项和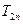 ;???(Ⅲ)若数列
;???(Ⅲ)若数列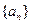 的前
的前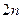 项和为
项和为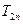 ,不等式
,不等式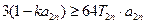 对
对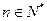 恒成立,求
恒成立,求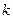 的最大值.
的最大值.(Ⅰ)略 (Ⅱ)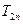
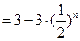 (Ⅲ)-48
(Ⅲ)-48
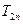
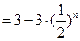 (Ⅲ)-48
(Ⅲ)-48:(1)∵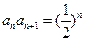 ,∴
,∴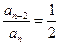
∴数列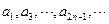 是以1为首项,
是以1为首项,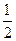 为公比的等比数列;
为公比的等比数列;
数列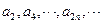 是以
是以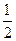 为首项,
为首项,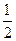 为公比的等比数列。
为公比的等比数列。
(2)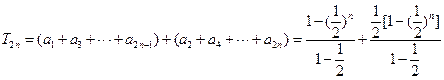
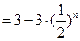
(3)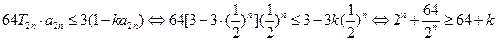
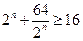 当且仅当
当且仅当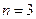 时取等号,所以
时取等号,所以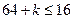 ,即
,即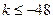 ,
,
∴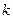 的最大值为-48
的最大值为-48
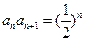 ,∴
,∴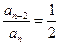
∴数列
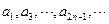 是以1为首项,
是以1为首项,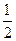 为公比的等比数列;
为公比的等比数列;数列
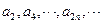 是以
是以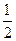 为首项,
为首项,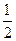 为公比的等比数列。
为公比的等比数列。(2)
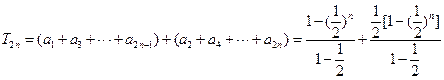
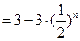
(3)
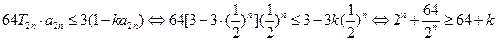
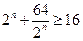 当且仅当
当且仅当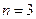 时取等号,所以
时取等号,所以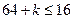 ,即
,即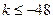 ,
,∴
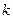 的最大值为-48
的最大值为-48
练习册系列答案
相关题目
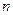 次操作后剩余图形的总面积为
次操作后剩余图形的总面积为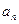
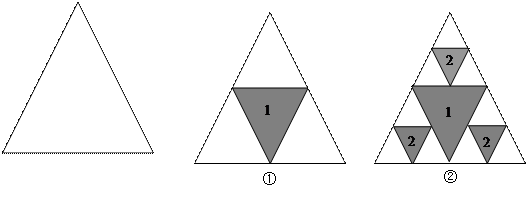
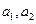 ;(2)求第
;(2)求第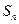 ;
;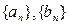 满足:
满足:
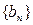 的通项公式;
的通项公式;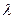 ,使得
,使得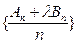 为等差数列?若存在,求出
为等差数列?若存在,求出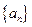 中,
中,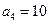 且
且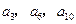 成等比数列,求数列
成等比数列,求数列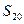 .
.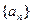 是等差数列,则( )
是等差数列,则( )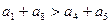 B
B 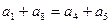
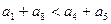 D
D 