题目内容
本题满分14分) 设函数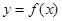 在
在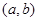 上的导函数为
上的导函数为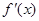 ,
,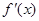 在
在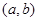 上的导函数为
上的导函数为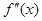 .若在
.若在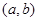 上,有
上,有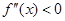 恒成立,则称函数
恒成立,则称函数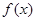 在
在
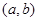 上为“凸函数”.已知
上为“凸函数”.已知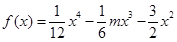 .
.
(Ⅰ) 若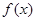 为区间
为区间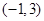 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数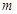 的值;
的值;
(Ⅱ) 若当实数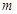 满足
满足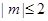 时,函数
时,函数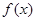 在
在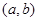 上总为“凸函数”,求
上总为“凸函数”,求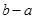 的最大值.
的最大值.
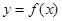 在
在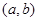 上的导函数为
上的导函数为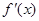 ,
,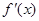 在
在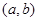 上的导函数为
上的导函数为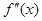 .若在
.若在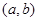 上,有
上,有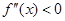 恒成立,则称函数
恒成立,则称函数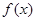 在
在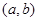 上为“凸函数”.已知
上为“凸函数”.已知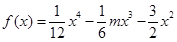 .
.(Ⅰ) 若
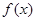 为区间
为区间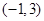 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数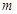 的值;
的值;(Ⅱ) 若当实数
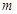 满足
满足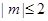 时,函数
时,函数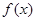 在
在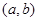 上总为“凸函数”,求
上总为“凸函数”,求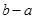 的最大值.
的最大值.解:由函数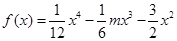 得,
得,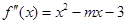 (3分)
(3分)
(Ⅰ) 若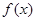 为区间
为区间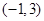 上的“凸函数”,则有
上的“凸函数”,则有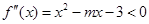 在区间
在区间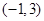 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当
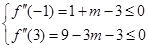 ,
,
即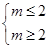
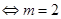 . (7分)
. (7分)
(Ⅱ)当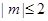 时,
时,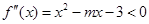 恒成立
恒成立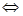 当
当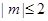 时,
时,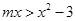 恒成立. (8分)
恒成立. (8分)
当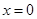 时,
时,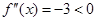 显然成立 (9分)
显然成立 (9分)
当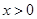 ,
,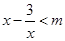 ∵
∵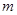 的最小值是
的最小值是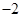 .∴
.∴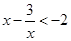 .
.
从而解得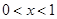 (11分)
(11分)
当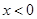 ,
,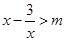 ∵
∵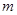 的最大值是
的最大值是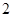 ,∴
,∴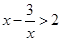 ,
,
从而解得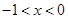 .
.
综上可得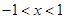 ,从而
,从而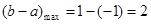 (14分)
(14分)
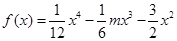 得,
得,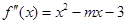 (3分)
(3分)(Ⅰ) 若
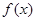 为区间
为区间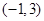 上的“凸函数”,则有
上的“凸函数”,则有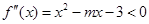 在区间
在区间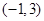 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当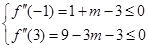 ,
,即
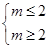
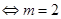 . (7分)
. (7分)(Ⅱ)当
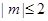 时,
时,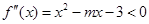 恒成立
恒成立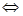 当
当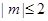 时,
时,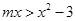 恒成立. (8分)
恒成立. (8分)当
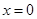 时,
时,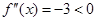 显然成立 (9分)
显然成立 (9分)当
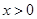 ,
,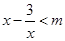 ∵
∵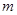 的最小值是
的最小值是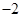 .∴
.∴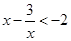 .
.从而解得
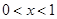 (11分)
(11分)当
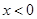 ,
,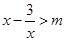 ∵
∵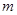 的最大值是
的最大值是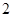 ,∴
,∴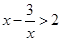 ,
,从而解得
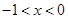 .
. 综上可得
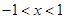 ,从而
,从而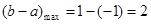 (14分)
(14分)略

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
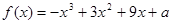 ,
,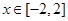 的最大值为20,则最小值是( )
的最大值为20,则最小值是( )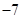
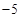
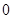
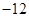
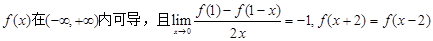 ,则
,则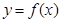 在点(-5,
在点(-5,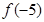 )处切线的斜率为( )
)处切线的斜率为( )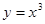 在点(2,8)处的切线方程为_______________________。
在点(2,8)处的切线方程为_______________________。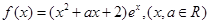 其中
其中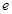 为自然对数的底数
为自然对数的底数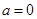 时,求曲线
时,求曲线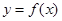 在
在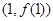 处的切线方程;
处的切线方程;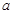 的取值范围;
的取值范围;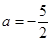 时,求函数
时,求函数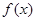 的极小值。
的极小值。 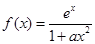 ,其中
,其中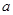 为正实数.
为正实数.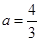 时,求
时,求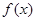 的极值点;
的极值点;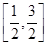 上的单调函数,求
上的单调函数,求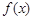 的定义域为开区间
的定义域为开区间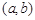 ,导函数
,导函数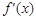 在
在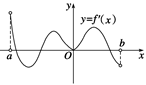
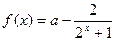 ,
,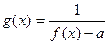
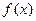 为奇函数,求
为奇函数,求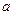 的值。
的值。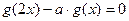 ,有唯一实数解,求
,有唯一实数解,求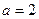 ,则是否存在实数
,则是否存在实数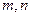 (
(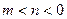 ),使得函数
),使得函数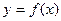 的定义域和值域都为
的定义域和值域都为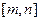 。若存在,求出
。若存在,求出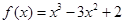 在区间[-1,1]上的极大值是 ( )
在区间[-1,1]上的极大值是 ( )