题目内容
17.计算:$\sqrt{23-6\sqrt{10-4\sqrt{3+2\sqrt{2}}}}$=3+$\sqrt{2}$.分析 利用根式的意义及其运算性质、乘法公式即可得出.
解答 解:原式=$\sqrt{23-6\sqrt{10-4(\sqrt{2}+1)}}$
=$\sqrt{23-6\sqrt{6-2\sqrt{8}}}$
=$\sqrt{23-6(2-\sqrt{2})}$
=$\sqrt{11+2\sqrt{18}}$
=3+$\sqrt{2}$.
故答案为:3+$\sqrt{2}$.
点评 本题考查了根式的意义及其运算性质、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
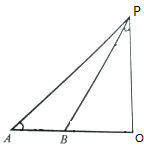 如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).
如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).