Question

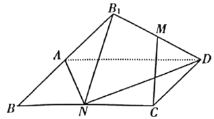
【题目】如图，四棱锥O﹣ABCD的底面是边长为1的菱形，OA＝2，∠ABC＝60°，OA⊥平面ABCD，M、N分别是OA、BC的中点.

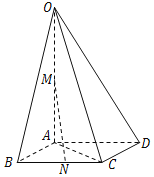
（1）求证：直线MN∥平面OCD；

（2）求点M到平面OCD的距离.

Answer 1

【答案】（1）证明见解析（2）

【解析】

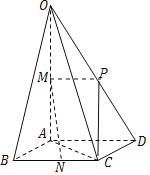
（1）取OD的中点P，连接PC、PM，由三角形的中位线定理可得PMNC是平行四边形，得MN∥PC，再由直线与平面平行的判定可得直线MN∥平面OCD；

（2）连接ON、ND，设点M到平面OCD的距离为d，可得点N到平面OCD的距离为d，然后利用等体积法求点M到平面OCD的距离.

（1）证明：取OD的中点P，连接PC、PM，

∵M、N分别是OA、BC的中点，∴PM∥AD，且，NC∥AD，且，

∴PM∥NC，且PM＝NC，则PMNC是平行四边形，得MN∥PC，

∵PC平面OCD，MN平面OCD，

∴直线MN∥平面OCD；

（2）解：连接ON、ND，设点M到平面OCD的距离为d，

由（1）得，点N到平面OCD的距离为d，

设三棱锥O﹣CDN的体积为V，则，

依题意，，

∵AC＝AD＝CD＝1，∴，则.

由，得点M到平面OCD的距离.