题目内容
12.某投资人打算投资甲、乙两个项目,根据预测:甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别是30%和10%,投资人计划投资额不超过10万,要求确保可能的资金亏损不超过1.8万元.若要使可能的盈利最大,则投资人对甲、乙两个项目应各自投资4、6万元.分析 通过设投资人分别用x万元、y万元投资甲、乙两个项目,得出可行域,进而利用目标函数z=x+0.5y计算即得结论.
解答 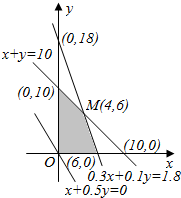 解:设投资人分别用x万元、y万元投资甲、乙两个项目,
解:设投资人分别用x万元、y万元投资甲、乙两个项目,
由题意知,$\left\{\begin{array}{l}{x+y≤10}\\{0.3x+0.1y≤1.8}\\{x≥0}\\{y≥0}\end{array}\right.$,
目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示,阴影部分(含边界)即可行域.
作直线l0:x+0.5y=0,并作平行于直线l0的一组直线x+0.5y=z,z∈R,与可行域相交,
其中有一条直线经过可行域上的M点,且与直线x+0.5y=0的距离最大,
这里M点是直线x+y=10和0.3x+0.1y=1.8的交点.
联立方程组$\left\{\begin{array}{l}{x+y=10}\\{0.3x+0.1y=1.8}\end{array}\right.$,解得x=4,y=6.
∴当x=4、y=6时,z取得最大值zmax=4+6×0.5=7(万元).
∴投资人可能产生的最大盈利为7万元,
故答案为:4、6.
点评 本题考查简单线性规划,考查数形结合能力,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.函数$f(x)=1o{g_{\frac{1}{2}}}(2{x^2}-ax+3)$在区间[-1,+∞)上是减函数,则实数a的取值范围是( )
| A. | (-∞,-5)∪[-4,+∞) | B. | (-5,-4] | C. | (-∞,-4] | D. | [-4,0) |
7.函数f(x)是定义在R上的奇函数,且它是减函数,若实数a,b满足f(a)+f(b)>0,则a与b的关系是( )
| A. | a+b>0 | B. | a+b<0 | C. | a+b=0 | D. | 不确定 |
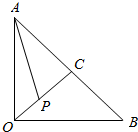 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.