题目内容
17.已知二次函数f(x)的最小值为1,且f(0)=f(2)=3(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上是单调函数,求实数a的取值范围.
分析 (1)根据二次函数f(x)的最小值为1,且f(0)=f(2)可得对称轴为x=1,可设f(x)=a(x-1)2+1,由f(0)=3,求出a的值即可;
(2)根据 f(x)在区间[2a,a+1]上是单调函数则对称轴应该在区间的左侧或在区间的右侧,从而可求出a的取值范围.
解答 解:(1)由已知,设f(x)=a(x-1)2+1,由f(0)=3,得a=2,
故f(x)=2x2-4x+3;
(2)二次函数的对称轴为x=1,
当对称轴在区间的左侧时,
函数f(x)在区间[2a,a+1]上单调递增,即2a≥1解得a≥$\frac{1}{2}$;
当对称轴在区间的右侧时,
函数f(x)在区间[2a,a+1]上单调递减,即a+1≤1解得a≤0,
综上,实数a的取值范围为(-∞,0]∪[$\frac{1}{2}$,+∞).
点评 本题主要考查了二次函数的性质,以及二次函数在闭区间上的单调性,同时考查了分类讨论的数学思想,属于中档题..

练习册系列答案
相关题目
7.如图所示,程序框图输出的结果为( )
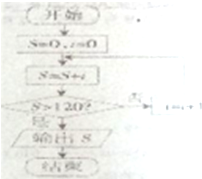

| A. | 15 | B. | 16 | C. | 136 | D. | 153 |
2.已知等差数列{an}的前n项和为Sn,且a2=18-a7,S8=( )
| A. | 18 | B. | 36 | C. | 54 | D. | 72 |
9.定义域为R的连续函数f(x)对任意x都有f(x)=f(4-x),且当x≠2时,其导函数满足(x-2)•f′(x)>0,则有( )
| A. | f(sinx)<f(1+sinx)<f(52+sinx) | B. | f(52+sinx)<f(sinx)<f(1+sinx) | ||
| C. | f(1+sinx)<f(sinx)≤f(52+sinx) | D. | f(1+sinx)<f(52+sinx)≤f(sinx) |
7.12个同类产品中含有2个次品,现从中任意抽出3个,必然事件是( )
| A. | 3个都是正品 | B. | 至少有一个是次品 | ||
| C. | 3个都是次品 | D. | 至少有一个是正品 |