题目内容
3.函数$f(x)=1o{g_{\frac{1}{2}}}(2{x^2}-ax+3)$在区间[-1,+∞)上是减函数,则实数a的取值范围是( )| A. | (-∞,-5)∪[-4,+∞) | B. | (-5,-4] | C. | (-∞,-4] | D. | [-4,0) |
分析 利用换元法,结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=g(x)=2x2-ax+3,则t=log${\;}_{\frac{1}{2}}$t为减函数,
若函数$f(x)=1o{g_{\frac{1}{2}}}(2{x^2}-ax+3)$在区间[-1,+∞)上是减函数,
则等价为t=g(x)在区间[-1,+∞)上是增函数,
且满足g(-1)>0,
即$\left\{\begin{array}{l}{-\frac{-a}{2×2}=\frac{a}{4}≤-1}\\{2+a+3>0}\end{array}\right.$,即$\left\{\begin{array}{l}{a≤-4}\\{a>-5}\end{array}\right.$,
即-5<a≤4,
故选:B.
点评 本题主要考查复合函数单调性的应用,利用换元法结合一元二次函数的单调性的性质是解决本题的关键.

练习册系列答案
相关题目
15.在△ABC中,角A,B,C所对的边分别是a,b,c,已知 sin(B+C)+sin(B-C)=2sin2C,且a=4,A=$\frac{π}{3}$,则△ABC的面积是( )
| A. | $\frac{8\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{4}$ | C. | $\frac{8}{3}$ | D. | $\frac{8\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{4}$ |

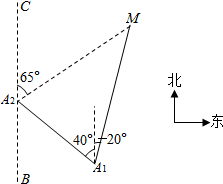 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.