题目内容
1.计算:$\underset{lim}{x→∞}$$\frac{{2x}^{2}+3}{3x+2}$sin$\frac{1}{x}$=$\frac{2}{3}$.分析 化简$\underset{lim}{x→∞}$$\frac{{2x}^{2}+3}{3x+2}$sin$\frac{1}{x}$=$\underset{lim}{x→∞}$$\frac{sin\frac{1}{x}}{\frac{3x+2}{2{x}^{2}+3}}$=$\underset{lim}{x→∞}$$\frac{\frac{1}{x}}{\frac{3x+2}{2{x}^{2}+3}}$,从而解得.
解答 解:$\underset{lim}{x→∞}$$\frac{{2x}^{2}+3}{3x+2}$sin$\frac{1}{x}$
=$\underset{lim}{x→∞}$$\frac{sin\frac{1}{x}}{\frac{3x+2}{2{x}^{2}+3}}$
=$\underset{lim}{x→∞}$$\frac{\frac{1}{x}}{\frac{3x+2}{2{x}^{2}+3}}$
=$\underset{lim}{x→∞}$$\frac{2{x}^{2}+3}{3{x}^{2}+2x}$
=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了洛必达法则的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.定义域为R的连续函数f(x)对任意x都有f(x)=f(4-x),且当x≠2时,其导函数满足(x-2)•f′(x)>0,则有( )
| A. | f(sinx)<f(1+sinx)<f(52+sinx) | B. | f(52+sinx)<f(sinx)<f(1+sinx) | ||
| C. | f(1+sinx)<f(sinx)≤f(52+sinx) | D. | f(1+sinx)<f(52+sinx)≤f(sinx) |
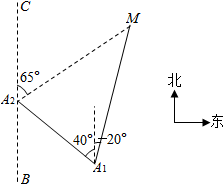 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.