题目内容
7．函数f（x）是定义在R上的奇函数，且它是减函数，若实数a，b满足f（a）+f（b）＞0，则a与b的关系是（ ）| A． | a+b＞0 | B． | a+b＜0 | C． | a+b=0 | D． | 不确定 |
分析 根据函数奇偶性和单调性的关系进行判断即可．
解答 解：由f（a）+f（b）＞0得f（a）＞-f（b），
∵f（x）是奇函数，
∴-f（b）=f（-b），
即不等式等价为得f（a）＞f（-b），
∵f（x）是减函数，
∴a＜-b，
即a+b＜0，
故选：B
点评 本题主要考查函数单调性的应用，结合函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
17．
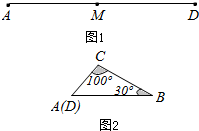如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）
如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）| A． | 点M在AB上 | |
| B． | 点M在BC的中点处 | |
| C． | 点M在BC上，且距点B较近，距点C较远 | |
| D． | 点M在BC上，且距点C较近，距点B较远 |
15．在△ABC中，角A，B，C所对的边分别是a，b，c，已知 sin（B+C）+sin（B-C）=2sin2C，且a=4，A=$\frac{π}{3}$，则△ABC的面积是（ ）
| A． | $\frac{8\sqrt{3}}{3}$ | B． | $\frac{8\sqrt{3}}{4}$ | C． | $\frac{8}{3}$ | D． | $\frac{8\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{4}$ |
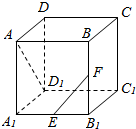长方体ABCD-A1B1C1D1中，AB=BC=2a，AA1=a，E和F分别是A1B1和BB1的中点，求：