题目内容
已知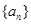 为等差数列,且
为等差数列,且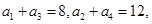
(1)求数列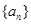 的通项公式;
的通项公式;
(2)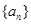 的前
的前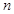 项和为
项和为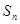 ,若
,若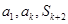 成等比数列,求正整数
成等比数列,求正整数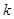 的值。
的值。
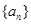 为等差数列,且
为等差数列,且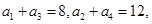
(1)求数列
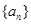 的通项公式;
的通项公式;(2)
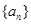 的前
的前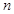 项和为
项和为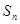 ,若
,若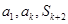 成等比数列,求正整数
成等比数列,求正整数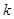 的值。
的值。(1)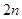 (2)
(2)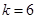
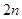 (2)
(2)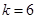
本试题主要是考查了数列的通项公式的求解和数列求和的运用。
(1)设数列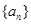 的公差为d,由题意知
的公差为d,由题意知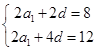 联立方程组,得到通项公式。
联立方程组,得到通项公式。
(2)由(Ⅰ)可得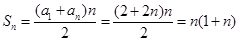
因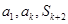 成等比数列,所以
成等比数列,所以 ,从而得到求解。
,从而得到求解。
解:(1)设数列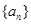 的公差为d,由题意知
的公差为d,由题意知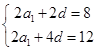 解得
解得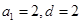 ……3分
……3分
所以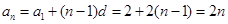 …………5分
…………5分
(2)由(Ⅰ)可得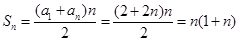 …………8分
…………8分
因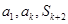 成等比数列,所以
成等比数列,所以
从而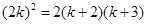 ,即
,即 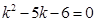 …………10分
…………10分
解得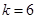 或
或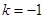 (舍去),
(舍去),
因此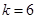 。…………12分
。…………12分
(1)设数列
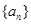 的公差为d,由题意知
的公差为d,由题意知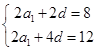 联立方程组,得到通项公式。
联立方程组,得到通项公式。(2)由(Ⅰ)可得
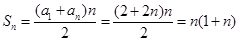
因
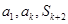 成等比数列,所以
成等比数列,所以 ,从而得到求解。
,从而得到求解。解:(1)设数列
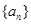 的公差为d,由题意知
的公差为d,由题意知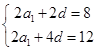 解得
解得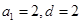 ……3分
……3分所以
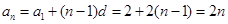 …………5分
…………5分(2)由(Ⅰ)可得
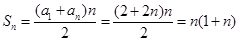 …………8分
…………8分因
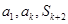 成等比数列,所以
成等比数列,所以
从而
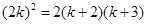 ,即
,即 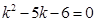 …………10分
…………10分解得
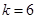 或
或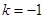 (舍去),
(舍去),因此
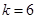 。…………12分
。…………12分
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 中,公差
中,公差 又
又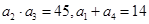 .
.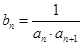 ,数列
,数列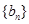 的前
的前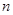 项和记为
项和记为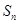 ,求
,求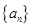 中,
中,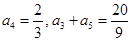 .
.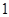 ,且
,且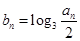 ,求数列
,求数列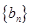 的前
的前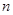 项和
项和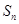 .
.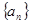 的前
的前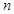 项和为
项和为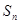 ,且
,且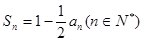
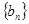 的通项公式
的通项公式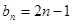 ,记
,记 ,求数列
,求数列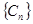 的前
的前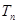 .
.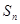 ﹥0成立的最大自然数n的值为.
﹥0成立的最大自然数n的值为. 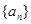 的前
的前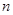 项和为
项和为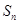 ,已知
,已知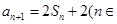 N
N ).
).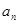 与
与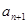 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为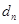 的等差数列,求数列
的等差数列,求数列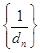 的前
的前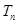 .(6分)
.(6分)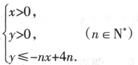 表示的平面区域为
表示的平面区域为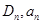 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则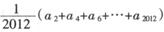 =( )
=( )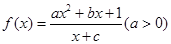 为奇函数,且
为奇函数,且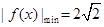 ,数列
,数列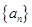 与
与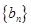 满足如下关系:
满足如下关系: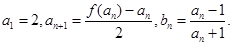
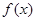 的解析式;
的解析式;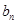 ;
;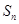 为数列
为数列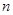 项和,求证:对任意的
项和,求证:对任意的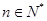 有
有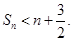
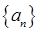 的前n项和为
的前n项和为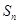 ,且
,且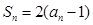 ,则
,则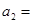 _______.
_______.