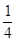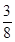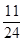题目内容
某校周四下午第五、六两节是选修课时间,现有甲、乙、丙、丁四位教师可开课。已知甲、乙教师各自最多可以开设两节课,丙、丁教师各自最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则不同的开课方案共有( )种。
| A.20 | B.19 | C.16 | D.15 |
B
解析试题分析:法一:枚举可得,有下列的开课方案:
(1)第五节:甲,乙,第六节:甲,乙;(2)第五节:甲,乙,第六节:甲,丙(丁);(两种)
(3)第五节:甲,乙,第六节:乙,丙(丁);(两种)(4)第五节:甲,丙(丁),第六节:甲,乙;(两种)(5)第五节:乙,丙(丁),第六节:甲,乙;(两种)(6)第五节:甲,乙,第六节:丙,丁;(7)第五节:甲,丙,第六节:甲,丁;(8)第五节:甲,丙,第六节:乙,丁;(9)第五节:乙,丙,第六节:甲,丁;(10)第五节:乙,丙,第六节:乙,丁;(11)第五节:甲,丁,第六节:甲,丙;(12)第五节:甲,丁,第六节:乙,丙;(13)第五节:乙,丁,第六节:甲,丙;(14)第五节:乙,丁,第六节:乙,丙;(15)第五节:丙,丁,第六节:甲,乙;
综上所述,一共有19种开课方案.
法二:开课方案可以分一下几种情况:(1)丙丁都不上课,有1种方案;(2)丙丁有一个老师上课,有(2+2)×2=8种方案;(3)丙丁老师都上课,有1+4+4+1=10种方案.根据分类加法计数原理可得共有1+8+10=19种开课方案.
考点:排列组合

在 的展开式中,x的幂指数是整数的项共有
的展开式中,x的幂指数是整数的项共有
| A.3项 | B.4项 | C.5项 | D.6项 |
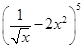 的展开式中常数项是( )
的展开式中常数项是( )
| A.5 | B.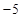 | C.10 | D. |
数列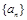 共有12项,其中
共有12项,其中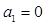 ,
,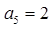 ,
, ,且
,且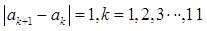 ,则满足这种条件的不同数列的个数为( )
,则满足这种条件的不同数列的个数为( )
| A.84 | B.168 | C.76 | D.152 |
用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )
| A.243 | B.252 | C.261 | D.279 |
在下列命题中, ①“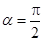 ”是“
”是“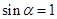 ”的充要条件;②
”的充要条件;② 的展开式中的常数项为
的展开式中的常数项为 ;③设随机变量
;③设随机变量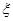 ~
~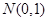 ,若
,若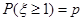 ,则
,则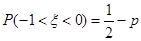 .其中所有正确命题的序号是( )
.其中所有正确命题的序号是( )
| A.② | B.②③ | C.③ | D.①③ |
从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有
| A.96种 | B.180种 | C.240种 | D.280种 |
某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有( )
| A.4种 | B.10种 |
| C.18种 | D.20种 |