题目内容
设集合A={x|0<x<1},B={x|0<x<3},那么“m∈A”是“m∈B”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:利用集合的包含关系,判断出集合M与N的关系,利用N是M的真子集,判断两者的关系.因为集合A={x|0<x<1},B={x|0<x<3},那么可知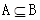 ,因此可知m∈A”是“m∈B”的充分不必要条件,选A.
,因此可知m∈A”是“m∈B”的充分不必要条件,选A.
考点:充分条件的判定
点评:本题考查利用集合的包含关系判断一个命题是另一个命题的什么条件.当A?B时,A是B的充分不必要条件.

练习册系列答案
相关题目
在△ABC中“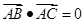 ”是“△ABC为直角三角形”的( ).
”是“△ABC为直角三角形”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出下面四个命题:
①分别与两条异面直线都相交的两条直线一定是异面直线;
②分别与两个平行平面都平行的两条直线一定平行;
③垂直于同一个平面的两条直线平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中为真命题的是( )
| A.①③ | B.①④ | C.③④ | D.②③ |
下列说法不正确的是( )
A.“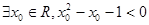 ”的否定是“ ”的否定是“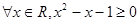 ” ” |
B.命题“若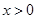 且 且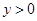 ,则 ,则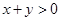 ”的否命题是假命题 ”的否命题是假命题 |
C.“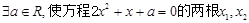 满足 满足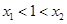 ”和“函数 ”和“函数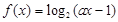 在[1,2]上单调递增”同时为真 在[1,2]上单调递增”同时为真 |
D.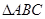 中 中 是最大角,则 是最大角,则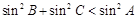 是 是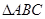 为钝角三角形的充要条件 为钝角三角形的充要条件 |
若命题p: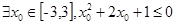 ,则对命题p的否定是( )
,则对命题p的否定是( )
A.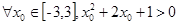 |
B.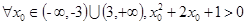 |
C.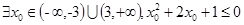 |
D.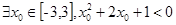 |
下列有关命题的说法错误的是 ( )
A.命题“若 则 则  ”的逆否命题为:“若 ”的逆否命题为:“若 , 则 , 则 ”. ”. |
B.“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
C.若 为假命题,则 为假命题,则 、 、 均为假命题. 均为假命题. |
D.对于命题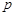 : : 使得 使得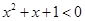 . 则 . 则 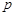 : : 均有 均有 |
已知直线a和两个平面 ,给出下列两个命题:
,给出下列两个命题:
命题p:若a∥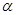 ,a⊥
,a⊥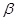 ,则
,则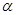 ⊥
⊥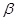 ;
;
命题q:若a∥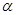 , a∥
, a∥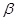 ,则
,则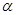 ∥
∥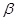 。
。
那么下列判断正确的是( )
| A.p为假 | B. 为假 为假 | C.p∧q为真 | D.p∨q为真 |
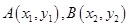 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: 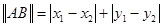 .给出下列三个命题:
.给出下列三个命题: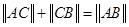 ;
;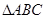 中,若∠C=90°,则
中,若∠C=90°,则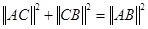 ;
;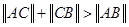 .
.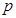 是
是 的充要条件的是
的充要条件的是 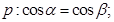
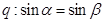 ;
;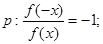
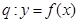 是奇函数;
是奇函数;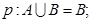
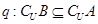 ;
;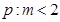 或
或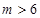 ;
;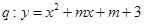 有两个不同的零点.
有两个不同的零点.