题目内容
在△ABC中“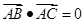 ”是“△ABC为直角三角形”的( ).
”是“△ABC为直角三角形”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:根据题意,由于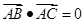 ∴-ac•cosα=0,即cosα=0,∵α∈(0,π)∴α=
∴-ac•cosα=0,即cosα=0,∵α∈(0,π)∴α= ,则△ABC为直角三角形;而当△ABC为直角三角形时,B不一定为直角,则
,则△ABC为直角三角形;而当△ABC为直角三角形时,B不一定为直角,则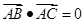 不一定成立,因此可知条件是结论成立的充分不必要条件,选A
不一定成立,因此可知条件是结论成立的充分不必要条件,选A
考点:三角形形状的判定
点评:此题考查了充分,必要及充要条件的判断,三角形形状的判断,涉及的知识有:平面向量的数量积运算法则,余弦函数的奇偶性,以及特殊角的三角函数值,熟练掌握法则及余弦函数的奇偶性是解本题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
有以下命题:①命题“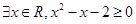 ”的否定是:“
”的否定是:“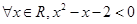 ”;
”;
②已知随机变量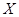 服从正态分布
服从正态分布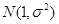 ,
,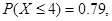 则
则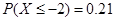 ;
;
③函数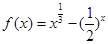 的零点在区间
的零点在区间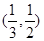 内;其中正确的命题的个数为( )
内;其中正确的命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
命题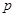 :函数
:函数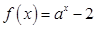 (
(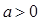 且
且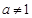 )的图像恒过点
)的图像恒过点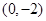 ;
;
命题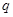 :函数
:函数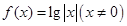 有两个零点.
有两个零点.
则下列说法正确的是
A.“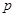 或 或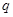 ”是真命题 ”是真命题 | B.“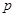 且 且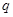 ”是真命题 ”是真命题 |
C.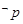 为假命题 为假命题 | D.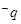 为真命题 为真命题 |
已知函数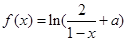 ,其中a为常数.则“
,其中a为常数.则“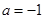 ”是f(x)为奇函数”的
”是f(x)为奇函数”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“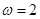 ”是“函数
”是“函数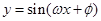 的最小正周期为
的最小正周期为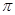 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题是真命题的为
A.若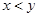 ,则 ,则 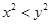 | B.若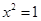 ,则 ,则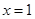 |
C.若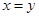 ,则 ,则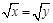 | D.若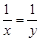 ,则 ,则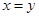 |
已知命题p: x∈R,x2+x一6
x∈R,x2+x一6 0,则命题
0,则命题 P是( )
P是( )
A. x∈R,x2+x一6>0 x∈R,x2+x一6>0 | B. x∈R.x2+x一6>0 x∈R.x2+x一6>0 |
C. x∈R,x2+x一6>0 x∈R,x2+x一6>0 | D. x∈R.x2+x一6<0 x∈R.x2+x一6<0 |
设集合A={x|0<x<1},B={x|0<x<3},那么“m∈A”是“m∈B”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
有关命题的说法错误的是
A.命题“若 ”的逆否命题为:“若 ”的逆否命题为:“若 ” ” |
B.“x=1”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.若 为假命题,则p、q均为假命题 为假命题,则p、q均为假命题 |
D.对于命题  ,则 ,则 |