题目内容
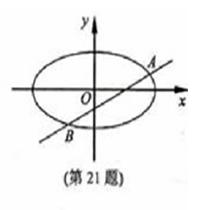
(本题满分15分)已知m>1,直线
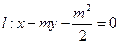 ,
,椭圆
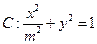 ,
,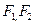 分别为椭圆
分别为椭圆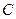 的左、右焦点.
的左、右焦点. (Ⅰ)当直线
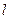 过右焦点
过右焦点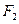 时,求直线
时,求直线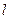 的方程;
的方程;(Ⅱ)设直线
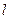 与椭圆
与椭圆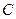 交于
交于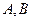 两点,
两点,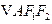 ,
,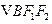 的重心分别为
的重心分别为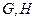 .若原点
.若原点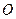 在以线段
在以线段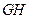 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围. 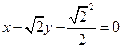 ,
,
(Ⅰ)解:因为直线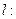
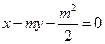 经过
经过 ,
,
所以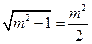 ,得
,得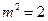 ,
,
又因为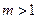 ,
,
所以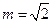 ,
,
故直线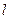 的方程为
的方程为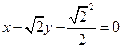 。
。
(Ⅱ)解:设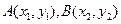 。
。
由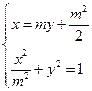 ,消去
,消去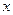 得
得
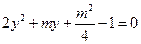
则由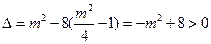 ,知
,知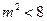 ,
,
且有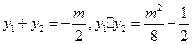 。
。
由于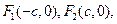 ,
,
故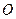 为
为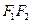 的中点,
的中点,
由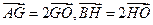 ,
,
可知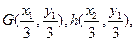
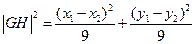
设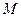 是
是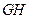 的中点,则
的中点,则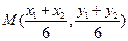 ,
,
由题意可知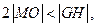
即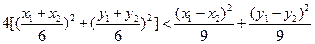
即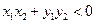
而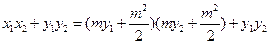
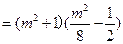
所以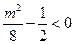
即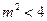
又因为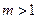 且
且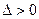
所以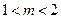 。
。
所以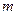 的取值范围是
的取值范围是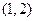 。
。
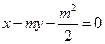 经过
经过 ,
,
所以
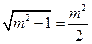 ,得
,得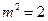 ,
,又因为
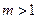 ,
,所以
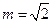 ,
,故直线
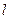 的方程为
的方程为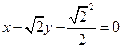 。
。(Ⅱ)解:设
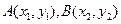 。
。由
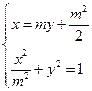 ,消去
,消去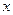 得
得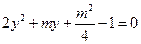
则由
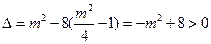 ,知
,知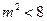 ,
,且有
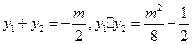 。
。由于
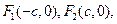 ,
,故
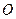 为
为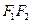 的中点,
的中点,由
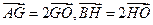 ,
,可知
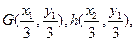
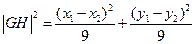
设
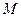 是
是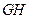 的中点,则
的中点,则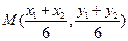 ,
,由题意可知
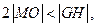
即
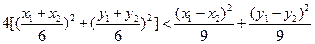
即
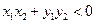
而
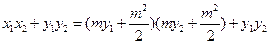
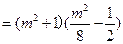
所以
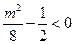
即
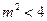
又因为
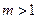 且
且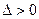
所以
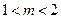 。
。所以
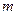 的取值范围是
的取值范围是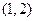 。
。
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
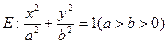 的两个焦点为
的两个焦点为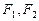 ,
,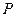 在椭圆
在椭圆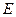 上,且
上,且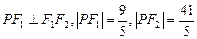 .
.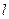 过圆
过圆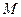
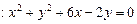 的圆心
的圆心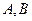 两点,且
两点,且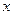 轴上,离心率为
轴上,离心率为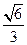 ,点
,点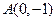 到F点的距离为
到F点的距离为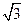 ,(1)求椭圆的方程;
,(1)求椭圆的方程;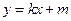 与椭圆交于不同的两点M、N两点,若
与椭圆交于不同的两点M、N两点,若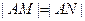 ,求实数
,求实数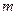 的取值范围。
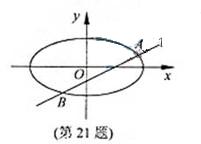
的取值范围。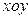 中,如图,已知椭圆
中,如图,已知椭圆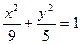 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T(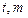 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M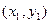 ,
,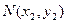 ,其中m>0,
,其中m>0,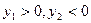
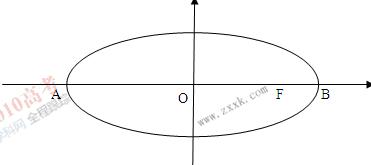
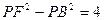 ,求点P的轨迹
,求点P的轨迹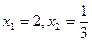 ,求点T的坐标
,求点T的坐标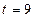 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点 轴上,若焦距为4,则m等于 ( )
轴上,若焦距为4,则m等于 ( )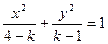 给出下面四个命题:
给出下面四个命题: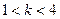 时,曲线C表示椭圆;
时,曲线C表示椭圆;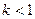 或
或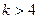
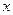 轴上的椭圆,则
轴上的椭圆,则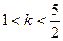
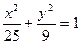 上任一点,F1、F2为椭圆的两焦点,若
上任一点,F1、F2为椭圆的两焦点,若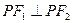 则
则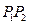 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?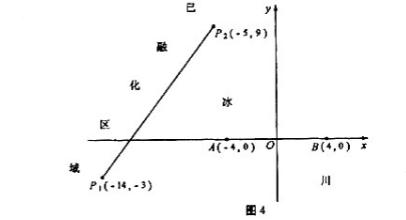
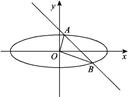
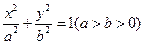 ,与直线
,与直线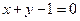 相交于
相交于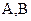 两点,且
两点,且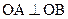 ,
,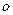 为坐标原点.
为坐标原点.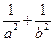 的值;
的值;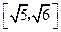 ,求椭圆离心率
,求椭圆离心率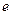 的取值范围.
的取值范围.