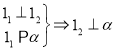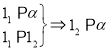题目内容
【题目】过点M（0，1）的直线l交椭圆C： 
于A，B两点，F1为椭圆的左焦点，当△ABF1周长最大时，直线l的方程为 ．
【答案】x+2y﹣2=0
【解析】解：设右焦点为F2（2，0），则AF1=6﹣AF2，BF1=6﹣BF2，
所以AF1+BF1+AB
=12+AB﹣（AF2+BF2），
显然AF2+BF2≥AB，
当且仅当A，B，F2共线时等号成立，
所以当直线l过点F2时，△ABF1的周长取最大值12，
此时直线方程为 
= 
，即x+2y﹣2=0．
所以答案是：x+2y﹣2=0
【考点精析】通过灵活运用椭圆的概念，掌握平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距即可以解答此题．
练习册系列答案
相关题目
