题目内容
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】分析:根据基本不等式,我们可以判断出“![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”与“对任意的正数x,2x+
≥1”与“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,进而根据充要条件的定义,即可得到结论.
解答:解:当“a=![]() ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+![]() ≥1”为真命题;
≥1”为真命题;
而“对任意的正数x,2x+![]() ≥1的”时,可得“a≥
≥1的”时,可得“a≥![]() ”
”
即“对任意的正数x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”为假命题;
”为假命题;
故“a=![]() ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+![]() ≥1的”充分不必要条件
≥1的”充分不必要条件
故选A
【题型】单选题
【结束】
9
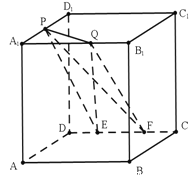
【题目】如图是一几何体的平面展开图,其中![]() 为正方形,
为正方形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,在此几何体中,给出下面四个结论:①直线
的中点,在此几何体中,给出下面四个结论:①直线![]() 与直线
与直线![]() 异面;②直线
异面;②直线![]() 与直线
与直线![]() 异面;③直线
异面;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .
.
其中一定正确的选项是( )

A. ①③ B. ②③ C. ②③④ D. ①③④
【答案】B
【解析】 如图所示:
①连接![]() ,则
,则![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,所以
,所以![]() ,
,
所以![]() 共面,所以直线
共面,所以直线![]() 与
与![]() 不是异面直线,所以错误;
不是异面直线,所以错误;
②因为![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
所以直线![]() 与直线
与直线![]() 是异面直线,所以是正确的;
是异面直线,所以是正确的;
③由①知![]() ,因为
,因为![]() 平面
平面![]() 平面
平面![]() ,所以直线
,所以直线![]() 平面
平面![]() ,所以正确;
,所以正确;
④假设平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
若![]() 时,必然平面
时,必然平面![]() 与平面
与平面![]() 不垂直,所以不正确,故选B.
不垂直,所以不正确,故选B.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案【题目】2016年一交警统计了某段路过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:
车速 |
|
|
|
|
|
事故次数 |
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(参考数据:![]() )
)
[参考公式: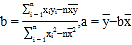 ]
]