题目内容
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间满足关系式
之间满足关系式![]() 为大于
为大于![]() 的常数),现随机抽取6件合格产品,测得数据如下:
的常数),现随机抽取6件合格产品,测得数据如下:

对数据作了处理,相关统计量的值如下表:

(1)根据所给数据,求![]() 关于
关于![]() 的回归方程(提示:由已知,
的回归方程(提示:由已知, ![]() 是
是![]() 的线性关系);
的线性关系);
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为 )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)对y=axb(a,b>0)两边取对数得lny=blnx+lna,令vi=lnxi,ui=lnyi得u=bv+lna,由最小二乘法求得系数![]() 及
及![]() ,即可求得y关于x的回归方程;
,即可求得y关于x的回归方程;
(Ⅱ)由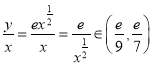 ,解得
,解得![]() ,
, ![]() ,即优等品有3件.
,即优等品有3件.
记“恰好取得两件优等品”为事件![]() ,从
,从![]() 件合格品中选出3件的方法数为
件合格品中选出3件的方法数为![]() ,
,
从![]() 件合格品取3件恰好2件为优等品的取法有
件合格品取3件恰好2件为优等品的取法有![]() 种,即可得恰好取得两件优等品的概率;
种,即可得恰好取得两件优等品的概率;
试题解析:
(1)对![]() ,两边取自然对数得
,两边取自然对数得![]() ,
,
令![]() ,得
,得![]() ,
,
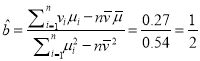 ,
, ![]() ,
,
得![]() ,故所求回归方程为
,故所求回归方程为![]() .
.
(2)由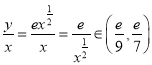 ,解得
,解得![]() ,
, ![]() ,即优等品有3件.
,即优等品有3件.
记“恰好取得两件优等品”为事件![]() ,从
,从![]() 件合格品中选出3件的方法数为
件合格品中选出3件的方法数为![]() ,
,
从![]() 件合格品取3件恰好2件为优等品的取法有
件合格品取3件恰好2件为优等品的取法有![]() 种,则
种,则![]() .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满足100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
(1)求![]() 的值并估计这100名考生成绩的平均分;
的值并估计这100名考生成绩的平均分;
(2)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;

