题目内容
【题目】已知不等式|x﹣3|+|x﹣4|<2a.
(1)若a=1,求不等式的解集;
(2)若已知不等式有解,求a的取值范围.
【答案】
(1)解:|x﹣3|+|x﹣4|<2,
①x≤3,则3﹣x+4﹣x<2,x> ![]() ,∴
,∴ ![]() <x≤3
<x≤3
②若3<x<4,则1<2,∴3<x<4.…(4分)
③若x≥4,则x﹣3+x﹣4<2,x< ![]() ,∴4≤x<
,∴4≤x< ![]()
综上,不等式的解集为( ![]() ,
, ![]() )
)
(2)解:|x﹣3|+|x﹣4|≥|x﹣3﹣x+4|=1,
∵不等式有解,∴2a>1,∴a> ![]() .)
.)
【解析】(1)分类讨论,即可求不等式的解集; (2)由条件利用绝对值三角不等式求得|x﹣3|+|x﹣4|≥|x﹣3﹣x+4|=1,结合题意可得a的范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
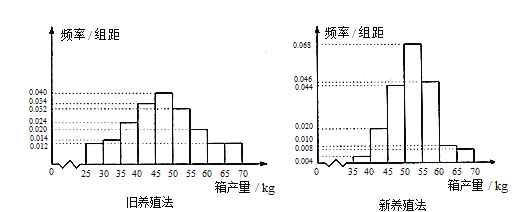
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: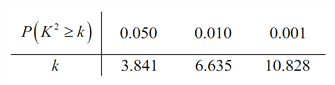 ,
, 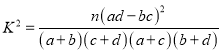
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟订的价格进行试销得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
(1)求出y关于x的线性回归方程 ![]() .其中
.其中 ![]() =250
=250
(2)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元每件,为使工厂获得最大利润,该产品的单价应定为多少元?