题目内容
已知 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 在点
在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的解析式;
的解析式;
(2)是否存在t∈N*,使得方程 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根?
若存在,求出t的值;若不存在,说明理由.
(1)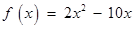 .
.
(2)存在唯一的自然数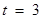 ,使得方程
,使得方程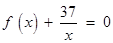 在区间
在区间 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.
解析试题分析:(1)根据 是二次函数,及不等式
是二次函数,及不等式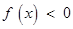 的解集是
的解集是 ,
,
可设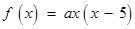 ,
, . 再根据函数在切点的斜率就是该点处的导函数值,可建立
. 再根据函数在切点的斜率就是该点处的导函数值,可建立
方程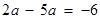 ,解得
,解得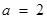 .
.
(2)首先由(1)知,方程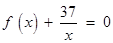 等价于方程
等价于方程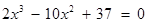 .
.
构造函数
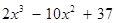 ,通过“求导数、求驻点、讨论导数值的正负”明确函数的单调区间,通过计算
,通过“求导数、求驻点、讨论导数值的正负”明确函数的单调区间,通过计算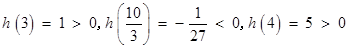 ,
,
认识方程有实根的情况.
试题解析:(1)∵ 是二次函数,不等式
是二次函数,不等式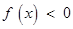 的解集是
的解集是 ,
,
∴可设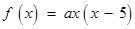 ,
, .
.
∴ . 2分
. 2分
∵函数 在点
在点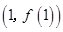 处的切线与直线
处的切线与直线 平行,
平行,
∴ .
.
∴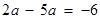 ,解得
,解得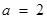 .
.
∴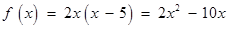 . 5分
. 5分
(2)由(1)知,方程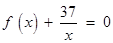 等价于方程
等价于方程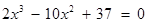 6分
6分
设
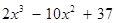 ,
,
则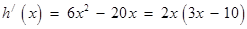 . 7分
. 7分
当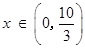 时,
时,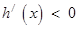 ,函数
,函数 在
在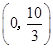 上单调递减;
上单调递减;
当 时,
时,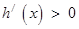 ,函数
,函数 在
在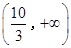 上单调递增. 9分
上单调递增. 9分
∵ ,
,
∴方程 在区间
在区间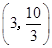 ,
, 内分别有唯一实数根,在区间
内分别有唯一实数根,在区间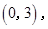
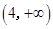 内没有实数根. 12分
内没有实数根. 12分
∴存在唯一的自然数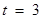 ,使得方程
,使得方程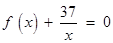
在区间 内有且只有两个不等的根. 13分
内有且只有两个不等的根. 13分
考点:二次函数,导数的几何意义,应用导数研究函数的单调性.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
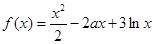
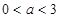 .
.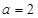 时,求函数
时,求函数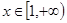 时,若
时,若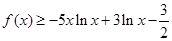 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 在(0,+∞)内的极值;
在(0,+∞)内的极值; ,
, ,且
,且 形成的平面区域的面积.
形成的平面区域的面积.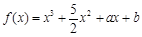 (
( 为常数),其图象是曲线
为常数),其图象是曲线 .
. 时,求函数
时,求函数 的单调减区间;
的单调减区间; ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围; 为曲线
为曲线 与曲线
与曲线 ,在点
,在点 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出 .
. 在
在 和
和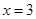 处的切线互相平行,求
处的切线互相平行,求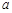 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意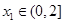 ,均存在
,均存在 ,使得
,使得 ,求
,求 ,其中
,其中 为常数.
为常数.  是区间
是区间 上的增函数,求实数
上的增函数,求实数 在
在 时恒成立,求实数
时恒成立,求实数 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. =
= 。
。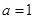 时,求函数
时,求函数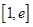 上的最小值;
上的最小值;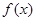 =
=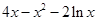 ,
,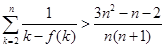 (
(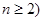 ),参考数据:
),参考数据: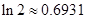 。(13分)
。(13分) 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t); ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值.