题目内容
已知函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)若函数 是区间
是区间 上的增函数,求实数
上的增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若 在
在 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)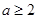 ;(Ⅱ)
;(Ⅱ)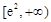
解析试题分析:(Ⅰ)函数 是区间
是区间 上的增函数,所以
上的增函数,所以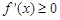 在
在 上恒成立。故应先求导,再求导函数的最小值使其大于等于
上恒成立。故应先求导,再求导函数的最小值使其大于等于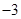 。(Ⅱ)
。(Ⅱ) 在
在 时恒成立即在
时恒成立即在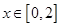 上
上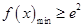 恒成立,故应去求函数
恒成立,故应去求函数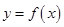 的最小值。应先求导,令导数等于0得
的最小值。应先求导,令导数等于0得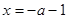 ,讨论导数的正负,得函数
,讨论导数的正负,得函数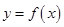 的单调区间。在讨论极值点
的单调区间。在讨论极值点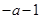 与0和2的大小得函数
与0和2的大小得函数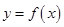 在
在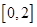 上的单调性,根据单调性求函数
上的单调性,根据单调性求函数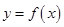 在
在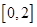 的最小值。
的最小值。
试题解析:(Ⅰ) ,
,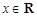 . 2分
. 2分
因为函数 是区间
是区间 上的增函数,
上的增函数,
所以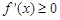 ,即
,即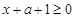 在
在 上恒成立. 3分
上恒成立. 3分
因为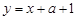 是增函数,
是增函数,
所以满足题意只需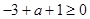 ,即
,即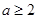 . 5分
. 5分
(Ⅱ)令 ,解得
,解得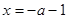 6分
6分 的情况如下:
的情况如下:
①当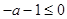 ,即
,即 时,
时, 在
在 上的最小值为
上的最小值为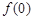 ,
,
若满足题意只需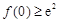 ,解得
,解得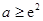 ,
,
所以此时,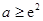 ; 11分
; 11分
②当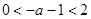 ,即
,即 时,
时, 在
在 上的最小值为
上的最小值为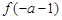 ,
,
若满足题意只需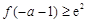 ,求解可得此不等式无解,
,求解可得此不等式无解,
所以 不存在; 12分
不存在; 12分
③当 ,即
,即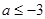 时,
时, 在
在 上的最小值为
上的最小值为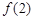 ,
,
若满足题意只需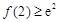 ,解得
,解得 ,
,
所以此时, 不存在. 13分
不存在. 13分
综上讨论,所求实数 的取值范围为
的取值范围为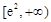 .
.
考点:考查导数和利用导数研究函数性质的方法的数学思想,意在考查考生灵活应用导数分析、解决问题的能力,考查考生的逻辑思维能力、运算能力和创新应用能力。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
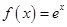 .
.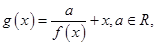 求
求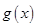 的极值.
的极值.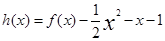 在
在 上为增函数。
上为增函数。 ,其中
,其中 是自然对数的底数,
是自然对数的底数,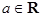 .
. 的单调区间;
的单调区间; 时,求函数
时,求函数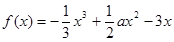 ,
,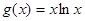
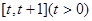 上的最小值;
上的最小值;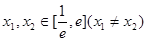 ,使方程
,使方程
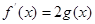 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数) 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.
平行. 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根?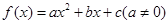 ,曲线
,曲线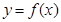 通过点(0,2a+3),且在
通过点(0,2a+3),且在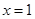 处的切线垂直于y轴.
处的切线垂直于y轴.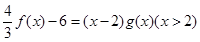 ,求g(x)的最大值及相应x值.
,求g(x)的最大值及相应x值.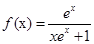 .
.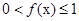 ;
;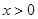 时,
时,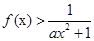 ,求
,求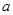 的取值范围.
的取值范围.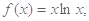
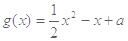 .
.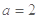 时,求
时,求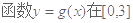 上的值域;
上的值域;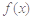 在
在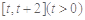 上的最小值;
上的最小值;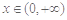 ,都有
,都有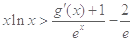 成立
成立