题目内容
设函数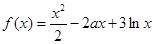
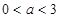 .
.
(1)当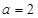 时,求函数
时,求函数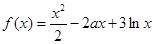 的单调区间;
的单调区间;
(2)当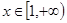 时,若
时,若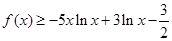 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)函数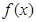 单调增区间为
单调增区间为 ,单调减区间为
,单调减区间为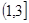 ;(2)
;(2)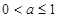 .
.
解析试题分析:(1)此类题目考查利用导数研究函数的单调性,解法是:求函数的导数,令导数大于零,解得单调增区间(注意函数的定义域),令导数小于零,解得单调减区间(注意定义域);(2)先将不等式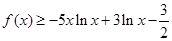 在
在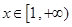 恒成立问题转化为
恒成立问题转化为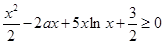 在
在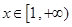 恒成立问题,然后可用两种方法求出参数的范围,法一是:令
恒成立问题,然后可用两种方法求出参数的范围,法一是:令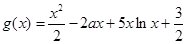 ,通过导数求出该函数的最小值,由这个最小值大于或等于0即可解出
,通过导数求出该函数的最小值,由这个最小值大于或等于0即可解出 的取值范围(注意题中所给的
的取值范围(注意题中所给的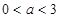 );法二是:先分离参数得
);法二是:先分离参数得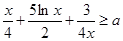 ,再令
,再令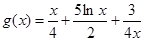 ,只须求出该函数的最小值
,只须求出该函数的最小值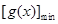 ,从而
,从而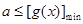 ,同时结合题中所给
,同时结合题中所给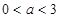 的范围可得参数
的范围可得参数 的取值范围.
的取值范围.
试题解析:(1)函数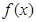 的定义域为
的定义域为 1分
1分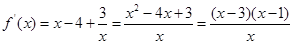 2分
2分
当 时,
时,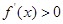 ,
,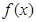 为增函数
为增函数
当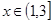 时,
时,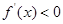 ,
,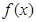 为减函数
为减函数
当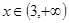 时,
时,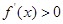 ,
,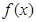 为增函数
为增函数
所以,函数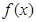 单调增区间为
单调增区间为 ,单调减区间为
,单调减区间为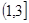 5分
5分
(2)因为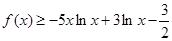 ,
,
所以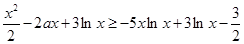
即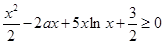
法一:令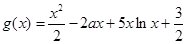 7分
7分
所以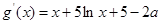
因为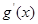 在
在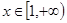 时是增函数 8分
时是增函数 8分
所以 9分
9分
又因为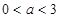 ,所以
,所以 , 10分
, 10分
所以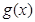 在
在 为增函数
为增函数
要使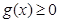 恒成立,只需
恒成立,只需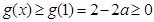 11分
11分
所以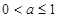 12分
12分
法二:因为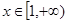 ,所以
,所以
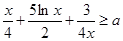 6
6
令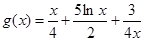 7分
7分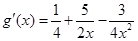
 8分
8分
因为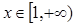 ,所以
,所以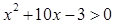 9分
9分
因此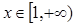 时,
时,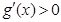 ,那么
,那么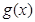 在
在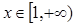 上为增函数 10分
上为增函数 10分
所以
所以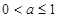 1
1

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
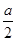 x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数). x2-
x2-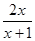 -
-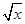 .
.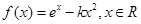 .
.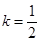 ,求证:当
,求证:当 时,
时, ;
; 在区间
在区间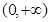 上单调递增,试求
上单调递增,试求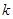 的取值范围;
的取值范围;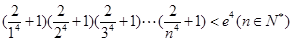 .
.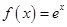 .
.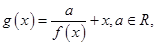 求
求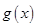 的极值.
的极值.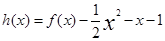 在
在 上为增函数。
上为增函数。 ,其中
,其中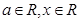 .
.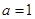 时,求函数
时,求函数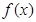 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; ,如果存在
,如果存在 ,使得函数
,使得函数
 在
在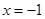 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值. .
. 在x=
在x= 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值; 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为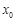 ,证明
,证明 .
. 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 处的切线与直线
处的切线与直线 平行.
平行. 在区间
在区间 内有两个不等的实数根?
内有两个不等的实数根?