题目内容
【题目】2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款,荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国.A地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区有6家婴幼儿用品商店在售这几种品牌的奶粉,甲、乙、丙3名检测员分别负责进行检测,每人至少抽检1家商店,且检测过的商店不重复检测,则甲检测员检测2家商店的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意分类讨论三人各检测的数量分配,求出所以情况的数量,再求出满足甲检测2家商店的情况数量,根据古典概型概率的求法即可求解.
若3人检测的数量为2:2:2,则所有的情况为![]() 种,
种,
若3人检测的数量为3:2:1,则所有的情况为![]() 种,
种,
若3人检测的数量为4:1:1,则所有的情况为![]() 种,
种,
故所有的情况为540种,其中满足甲检测2家商店的情况为![]() 种,
种,
故所求概率![]() .
.
故选:B

练习册系列答案
相关题目
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
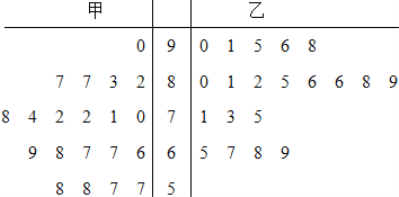
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
