题目内容
(12 分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .
分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .
(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)求该几何体的体积;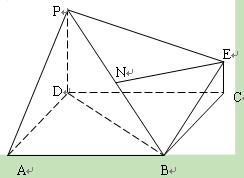
 分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .
分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)求该几何体的体积;

(1)证明:连结AC与BD交于点F, 连结NF,

∵F为BD的中点,N为PB的中点
∴ NF//PD且NF=
NF//PD且NF=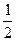 PD
PD
又EC//PD且 EC=
EC=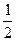 PD
PD
∴NF//EC且NF=EC
∴四边形NFCE为平行四边形
∴NE//FC
∵PD⊥平面ABCD,,AC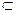 平面ABCD
平面ABCD
∴PD⊥AC, ∵AC⊥BD且PD ∩BD=D
∩BD=D
∴AC⊥平面PBD ∵EN//AC
∴NE⊥平面PBD
(2)∵PD⊥平面ABCD,,BC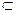 平面ABCD
平面ABCD
∴PD⊥BC,
∵BC⊥CD,平面PDCE∩平面DBC=CD ∴BC⊥平面PDCE
∵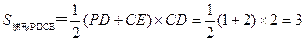
∴四棱锥B-CEPD的体积
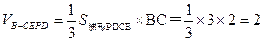
∵三棱锥P-ABD的体积
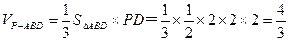

∵F为BD的中点,N为PB的中点
∴
 NF//PD且NF=
NF//PD且NF=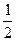 PD
PD又EC//PD且
 EC=
EC=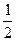 PD
PD∴NF//EC且NF=EC
∴四边形NFCE为平行四边形
∴NE//FC
∵PD⊥平面ABCD,,AC
 平面ABCD
平面ABCD∴PD⊥AC, ∵AC⊥BD且PD
 ∩BD=D
∩BD=D∴AC⊥平面PBD ∵EN//AC
∴NE⊥平面PBD
(2)∵PD⊥平面ABCD,,BC
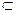 平面ABCD
平面ABCD ∴PD⊥BC,
∵BC⊥CD,平面PDCE∩平面DBC=CD ∴BC⊥平面PDCE
∵
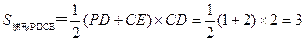
∴四棱锥B-CEPD的体积
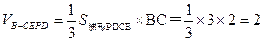
∵三棱锥P-ABD的体积
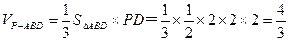
略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 B。
B。
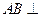 平面
平面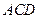 ,
,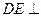 平面
平面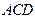 ,△
,△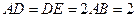 ,
, 为
为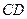 的中点.
的中点.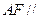 平面
平面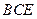 ;
;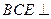 平面
平面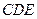 。
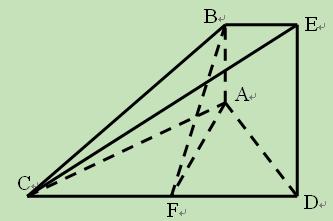
。
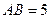 ,AA1=4,点D是AB的中点。
,AA1=4,点D是AB的中点。 的体积。
的体积。
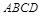 中,
中,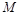 、
、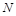 分别是
分别是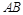 和
和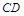 的中点,
的中点,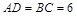 ,
,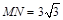 ,
,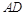 和
和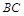 所成的角是( )
所成的角是( )