题目内容
(本小题满分14分)如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,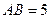 ,AA1=4,点D是AB的中点。
,AA1=4,点D是AB的中点。
(1)求证:AC ⊥ BC1;
(2)求证:AC 1 // 平面CDB1;
(3)求多面体 的体积。
的体积。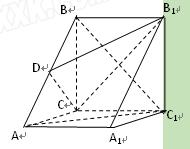
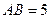 ,AA1=4,点D是AB的中点。
,AA1=4,点D是AB的中点。(1)求证:AC ⊥ BC1;
(2)求证:AC 1 // 平面CDB1;
(3)求多面体
 的体积。
的体积。
解:(1)∵底面三边长AC=3,BC=4,AB=5,∴AC⊥BC, (2分)
又在直三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC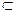 底面ABC,∴CC1⊥AC,(3
底面ABC,∴CC1⊥AC,(3 分)
分)
BC、 CC1
CC1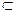 平面BCC1,且BC 与CC1相交 ∴ AC⊥平面BCC1;(5分)
平面BCC1,且BC 与CC1相交 ∴ AC⊥平面BCC1;(5分)
而BC1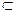 平面BCC1 ∴ AC⊥BC1 (6分)
平面BCC1 ∴ AC⊥BC1 (6分)
(2)设CB1与C1B的交点为E,连结DE,
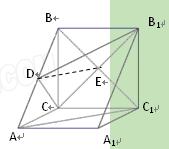
∵D是AB的中点,E是BC1的中点, ∴ D E//AC1, (8分)
E//AC1, (8分)
∵ DE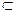 平面CDB1,AC1
平面CDB1,AC1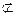 平面CDB1, ∴ AC1//平面CDB1 (10分)
平面CDB1, ∴ AC1//平面CDB1 (10分)
(3)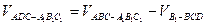 (11分)=
(11分)= -
-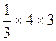 (13分)
(13分)
="20 " (14分)
又在直三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC
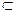 底面ABC,∴CC1⊥AC,(3
底面ABC,∴CC1⊥AC,(3 分)
分)BC、
 CC1
CC1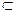 平面BCC1,且BC 与CC1相交 ∴ AC⊥平面BCC1;(5分)
平面BCC1,且BC 与CC1相交 ∴ AC⊥平面BCC1;(5分)而BC1
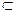 平面BCC1 ∴ AC⊥BC1 (6分)
平面BCC1 ∴ AC⊥BC1 (6分)(2)设CB1与C1B的交点为E,连结DE,

∵D是AB的中点,E是BC1的中点, ∴ D
 E//AC1, (8分)
E//AC1, (8分)∵ DE
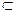 平面CDB1,AC1
平面CDB1,AC1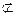 平面CDB1, ∴ AC1//平面CDB1 (10分)
平面CDB1, ∴ AC1//平面CDB1 (10分)(3)
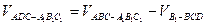 (11分)=
(11分)= -
-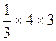 (13分)
(13分)="20 " (14分)
略

练习册系列答案
相关题目
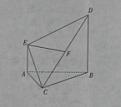
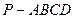 的底面
的底面 是正方形,侧棱
是正方形,侧棱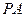
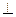 底面
底面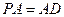 ,
,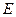 、
、 分别是棱
分别是棱 、
、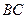 的中点.
的中点. 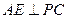 ; (2) 求直线
; (2) 求直线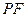 与平面
与平面 所成的角的正切值
所成的角的正切值
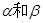 ,给定下列条件:
,给定下列条件: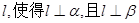 ;
; 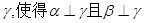 ;
;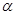 内有不共线的三点到
内有不共线的三点到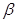 的距离相等;
的距离相等; 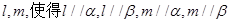
 平行的条件有 ( )
平行的条件有 ( ) 分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .
分)右图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC//PD,且PD=AD=2CE=2 .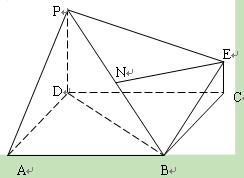
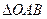 顶点
顶点 的坐标为
的坐标为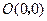 ,
,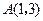 ,
,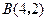 .
. 1)求点
1)求点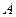 到直
到直 线
线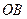 的距离
的距离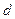 及
及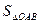 ;
;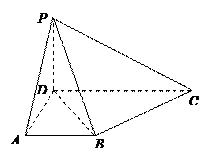
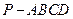 中,侧面
中,侧面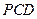
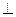 底面
底面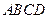 ,
,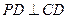 ,底面
,底面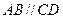 ,
,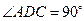 ,
,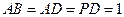 ,
,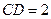 .
.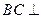 平面
平面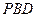 ;
;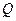 为侧棱
为侧棱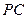 上一点,
上一点,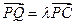 ,
,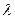 的值,使得二面角
的值,使得二面角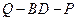 为
为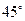 .
.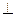 面ABC,AB
面ABC,AB