Question

【题目】已知⊙和点.过作⊙的两条切线，切点分别为且直线的方程为．

(1)求⊙的方程；

(2)设为⊙上任一点，过点向⊙引切线，切点为， 试探究：平面内是否存在一定点，使得为定值？若存在，请举出一例，并指出相应的定值；若不存在，请说明理由．

Answer 1

【答案】（1）（2）见解析

【解析】试题分析：（1）根据圆的切点弦方程可得，再与条件对比可得（2）为定值，可得P的轨迹方程，再与⊙方程对比可得参数，即得定值

试题解析：（1）以为直径的圆为： ，设圆的半径为，

故⊙的方程为，∴切点弦的方程为： ，

∴解得，故⊙的方程为．

（2）假设存在这样的点，点的坐标为，相应的定值为，

根据题意可得，∴，

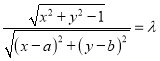即 （*），

又点在圆上∴，即，代入（*）式得：

，若系数对应相等，则等式恒成立，

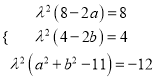∴，解得，

∴可以找到这样的定点，使得为定值. 如点的坐标为时，比值为；

点的坐标为时，比值为．