题目内容
【题目】选修4-4:坐标系与参数方程
已知圆![]() 和直线
和直线![]() .
.
(Ⅰ)求![]() 的参数方程以及圆
的参数方程以及圆![]() 上距离直线
上距离直线![]() 最远的点
最远的点![]() 坐标;
坐标;
(Ⅱ)以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,将圆
轴正半轴为极轴建立极坐标系,将圆![]() 上除点
上除点![]() 以外所有点绕着
以外所有点绕着![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() ,求曲线
,求曲线![]() 的极坐标方程.
的极坐标方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据![]() 可得
可得![]() 圆的参数方程,由直线的位置可得当
圆的参数方程,由直线的位置可得当![]() 时,圆
时,圆![]() 上的点距离直线
上的点距离直线![]() 最远,即可得点
最远,即可得点![]() 坐标;(Ⅱ)得
坐标;(Ⅱ)得![]() 的极坐标方程为
的极坐标方程为![]() ,该变换为
,该变换为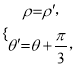 ,由相关点法可得结果.
,由相关点法可得结果.
试题解析:(Ⅰ) ![]() 的参数方程为
的参数方程为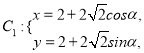 (
(![]() 为参数,
为参数, ![]() )
)
易得直线![]() 与圆
与圆![]() 均过坐标原点,且直线
均过坐标原点,且直线![]() 的倾斜角为
的倾斜角为![]() ,
,
所以当![]() 时,圆
时,圆![]() 上的点距离直线
上的点距离直线![]() 最远,
最远,
所以点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)由![]()
![]() 可得
可得![]() 的极坐标方程为
的极坐标方程为![]() ,
,
设![]() 上除极点外的某一点
上除极点外的某一点![]() 的极坐标为
的极坐标为![]() ,旋转后成为
,旋转后成为![]() ,
,
由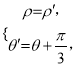 由相关点法,回代入
由相关点法,回代入![]() ,
,
可得![]() 的极坐标方程为
的极坐标方程为![]() .
.

练习册系列答案
相关题目


