题目内容
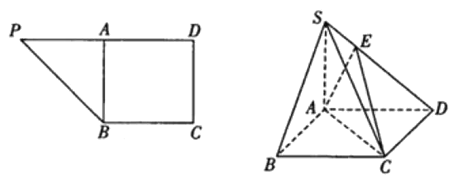
【题目】某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是 ![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() .
.
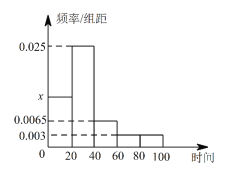
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)如果年上缴税收不少于![]() 万元的企业可申请政策优惠,若共抽取企业
万元的企业可申请政策优惠,若共抽取企业![]() 个,试估计有多少企业可以申请政策优惠;
个,试估计有多少企业可以申请政策优惠;
(Ⅲ)从企业中任选![]() 个,这
个,这![]() 个企业年上缴税收少于
个企业年上缴税收少于![]() 万元的个数记为
万元的个数记为 ![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率)
的分布列和数学期望.(以直方图中的频率作为概率)
【答案】(Ⅰ)![]() (Ⅱ)144(Ⅲ)分布列见解析,数学期望为1.
(Ⅱ)144(Ⅲ)分布列见解析,数学期望为1.
【解析】
(Ⅰ)根据频率分布直方图中各小长方体面积之和为1.列式求![]() 的值;(Ⅱ)先确定可以申请政策优惠的概率,再根据频数等于总数与频率的乘积得结果,(Ⅲ)先确定企业年上缴税收少于
的值;(Ⅱ)先确定可以申请政策优惠的概率,再根据频数等于总数与频率的乘积得结果,(Ⅲ)先确定企业年上缴税收少于![]() 万元的概率,再根据
万元的概率,再根据![]() 服从二项分布,确定分布列与数学期望.
服从二项分布,确定分布列与数学期望.
(Ⅰ)因为![]() ,
,
所以![]() ,
,
(Ⅱ)可以申请政策优惠的概率为![]() ,
,
所以企业有![]() 个,
个,
(Ⅲ)企业年上缴税收少于![]() 万元的概率为
万元的概率为![]()
![]()
![]()
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】某中学用简单随机抽样方法抽取了100名同学,对其社会实践次数进行调查,结果如下:
|
|
|
|
|
|
|
男同学人数 | 7 | 15 | 11 | 12 | 2 | 1 |
女同学人数 | 5 | 13 | 20 | 9 | 3 | 2 |
若将社会实践次数不低于12次的学生称为“社会实践标兵”.
(Ⅰ)将频率视为概率,估计该校1600名学生中“社会实践标兵”有多少人?
(Ⅱ)从已抽取的8名“社会实践标兵”中随机抽取4位同学参加社会实践表彰活动.
(i)设![]() 为事件“抽取的4位同学中既有男同学又有女同学”,求事件
为事件“抽取的4位同学中既有男同学又有女同学”,求事件![]() 发生的概率;
发生的概率;
(ii)用![]() 表示抽取的“社会实践标兵”中男生的人数,求随机变量
表示抽取的“社会实践标兵”中男生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.