题目内容
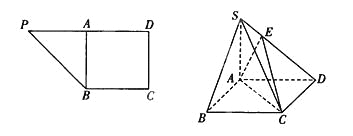
【题目】如图所示,在直角梯形ABCD中,已知![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
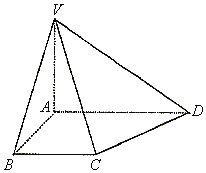
(1)求证:![]() 平面VAC;
平面VAC;
(2)若![]() ,求CV与平面VAD所成角的大小.
,求CV与平面VAD所成角的大小.
【答案】(1)见解析(2)![]()
【解析】
(1)证明连结AC,取AD中点G,连CG,证明四边形ABCG为正方形.推出![]() ,
,![]() ,即可证明
,即可证明![]() 平面VAC.
平面VAC.
(2)连VG,说明![]() 面VAD,
面VAD,![]() 是CV与平面VAD所成的角,通过求解三角形得到CV与平面VAD所成角为
是CV与平面VAD所成的角,通过求解三角形得到CV与平面VAD所成角为![]() .
.
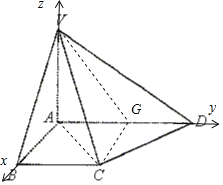
法2:以A为原点,射线AB,AD,AV所在直线为x,y,z轴正半轴,建立空间直角坐标系,平面VAD法向量![]() ,又
,又![]() ,利用空间向量的数量积求解即可.
,利用空间向量的数量积求解即可.
(1)证明:连结AC,∵![]() ,
,![]() ,∴
,∴![]() ,
,
取AD中点G,连CG,
因为![]() ,所以四边形ABCG为正方形.
,所以四边形ABCG为正方形.
所以![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]()
所以![]() ,
,
又![]() 平面ABCD,所以
平面ABCD,所以![]() ,
,
![]() 平面VAC
平面VAC
(2)解:法1:连VG
由![]()
![]()
![]() 面VAD,∴
面VAD,∴![]() 是CV与平面VAD所成的角
是CV与平面VAD所成的角
![]() ;
;![]() ,∴
,∴![]()
∴CV与平面VAD所成角为![]()
法2:以A为原点,射线AB,AD,AV所在直线为x,y,z轴正半轴,建立空间直角坐标系,则平面VAD法向量![]() ,又
,又![]() ,设向量
,设向量![]() 与
与![]() 夹角为
夹角为![]() ,则
,则![]() ,
,![]() ,CV与平面VAD所成的角为
,CV与平面VAD所成的角为![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
【题目】某校实行选科走班制度,张毅同学的选择是地理生物政治这三科,且生物在B层班级,该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有__________种
第一节 | 第二节 | 第三节 | 第四节 |
地理1班 | 化学A层3班 | 地理2班 | 化学A层4班 |
生物A层1班 | 化学B层2班 | 生物B层2班 | 历史B层1班 |
物理A层1班 | 生物A层3班 | 物理A层2班 | 生物A层4班 |
物理B层2班 | 生物B层1班 | 物理B层1班 | 物理A层4班 |
政治1班 | 物理A层3班 | 政治2班 | 政治3班 |