题目内容
【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),| ![]() |=1.
|=1.
(1)求 ![]() 与
与 ![]() 夹角;
夹角;
(2)若 ![]() 与
与 ![]() 垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| ![]() +
+ ![]() +
+ ![]() |的取值范围.
|的取值范围.
【答案】
(1)解:因为在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),所以 ![]() ,
,
![]() 与
与 ![]() 夹角的余弦值为
夹角的余弦值为 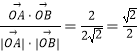 ,所以夹角为45°
,所以夹角为45°
(2)解:因为在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),所以 ![]() ,
,
设 ![]() =(x,y).因为
=(x,y).因为 ![]() 与
与 ![]() 垂直,又|
垂直,又| ![]() |=1.
|=1.
所以 ![]() ,解得
,解得 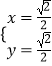 ,或
,或 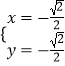 ,所以C
,所以C ![]() ,或C
,或C ![]() .
.
(3)解:由以上得到 ![]() +
+ ![]() +
+ ![]() =(3+x,1+y),|
=(3+x,1+y),| ![]() +
+ ![]() +
+ ![]() |2=(x+3)2+(y+1)2,又x2+y2=1,所以|
|2=(x+3)2+(y+1)2,又x2+y2=1,所以| ![]() +
+ ![]() +
+ ![]() |的最大值为
|的最大值为 ![]() ,最小值为
,最小值为 ![]()
【解析】(1)由已知,得到 ![]() 与
与 ![]() 的坐标,然后根据数量积求夹角;(2)由
的坐标,然后根据数量积求夹角;(2)由 ![]() 与
与 ![]() 垂直,得到数量积为0,得到点C的坐标的方程解之;(3)根据|
垂直,得到数量积为0,得到点C的坐标的方程解之;(3)根据| ![]() |=1,结合|
|=1,结合| ![]() +
+ ![]() +
+ ![]() |的几何意义求最值.
|的几何意义求最值.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目