题目内容
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n都有an是n与Sn的等差中项,bn=an+1.
(1)求证:数列{bn}是等比数列,并求出其通项bn;
(2)若数列{Cn}满足Cn= ![]() 且数列{C
且数列{C ![]() }的前n项和为Tn , 证明Tn<2.
}的前n项和为Tn , 证明Tn<2.
【答案】
(1)证明:∵an是n与的等差中项,
2an=n+Sn,
∴2an﹣1=n﹣1+Sn﹣1,(n≥2),
两式相减得:2an﹣2an﹣1=1+an,
an=2an﹣1+1,(n≥2),
∴an+1=2(an﹣1+1),
∴bn=2bn﹣1,
![]() =2,当n=1,2a1=1+S1,
=2,当n=1,2a1=1+S1,
∴a1=1,b1=2,
∴数列{bn}是等比数列是以2为首项,2为公比的等比数列,
bn=2n,
(2)证明:数列{Cn}满足Cn= ![]() =
= ![]() ,
,
∴C ![]() =
= ![]() ,
,
当n=1时,T1= ![]() =1<2,命题成立,
=1<2,命题成立,
当n≥2, ![]() ,
,
![]() <1+
<1+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,
=1+1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ,
,
=2﹣ ![]() <2,命题成立.
<2,命题成立.
【解析】(Ⅰ)由an是n与Sn的等差中项,2an=n+Sn , 当n≥2,2an﹣1=n﹣1+Sn﹣1 , 相减得:2an﹣2an﹣1=1+an , 化简整理得:an+1=2(an﹣1+1),bn=2bn﹣1 , b1=2,数列{bn}是等比数列是以2为首项,2为公比的等比数列;(Ⅱ)数列{Cn}满足Cn= ![]() ,C
,C ![]() =
= ![]() ,分类当n=1,
,分类当n=1, ![]() =1<2命题成立,当n≥2时,
=1<2命题成立,当n≥2时, ![]() <1+
<1+ ![]() +
+ ![]() +…+
+…+ ![]() ,采用裂项法,求得Tn=2﹣
,采用裂项法,求得Tn=2﹣ ![]() <2,命题成立.
<2,命题成立.
【考点精析】解答此题的关键在于理解等比数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系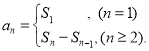 .
.

 名校课堂系列答案
名校课堂系列答案【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
