题目内容
( 12分)设函数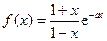 .
.
(1)写出定义域及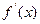 的解析式;
的解析式;
(2)设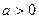 ,讨论函数
,讨论函数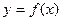 的单调性;
的单调性;
(3)若对任意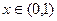 ,恒有
,恒有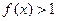 成立,求实数
成立,求实数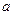 的取值范围.
的取值范围.
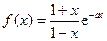 .
.(1)写出定义域及
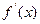 的解析式;
的解析式;(2)设
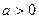 ,讨论函数
,讨论函数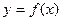 的单调性;
的单调性;(3)若对任意
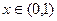 ,恒有
,恒有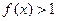 成立,求实数
成立,求实数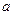 的取值范围.
的取值范围.解:(1)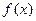 的定义域为
的定义域为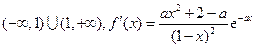 .
.
(2)①当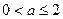 时,
时,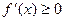 ,所以
,所以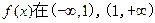 上为增函数;
上为增函数;
②当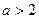 ,由
,由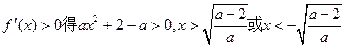 ,
,
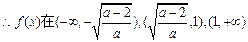 上为增函数,在
上为增函数,在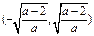 上是减函数.
上是减函数.
(3)①当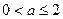 时,由(1)知,对任意
时,由(1)知,对任意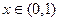 ,恒有
,恒有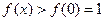 ;
;
②当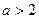 时,由(1)知,
时,由(1)知,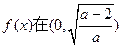 上是减函数,在
上是减函数,在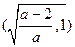 上是增函数,
上是增函数, 取
取
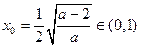 ,则
,则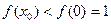 ;
;
③当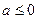 时,对任意
时,对任意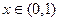 ,恒有
,恒有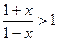 且
且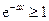 , 得
, 得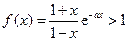 .
.
综上,当且仅当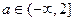 时,若对任意
时,若对任意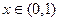 恒有
恒有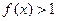 成立.
成立.
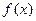 的定义域为
的定义域为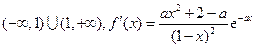 .
.(2)①当
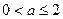 时,
时,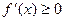 ,所以
,所以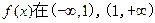 上为增函数;
上为增函数;②当
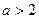 ,由
,由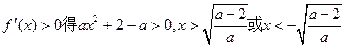 ,
,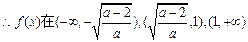 上为增函数,在
上为增函数,在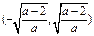 上是减函数.
上是减函数.(3)①当
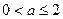 时,由(1)知,对任意
时,由(1)知,对任意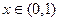 ,恒有
,恒有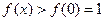 ;
;②当
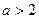 时,由(1)知,
时,由(1)知,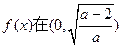 上是减函数,在
上是减函数,在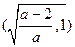 上是增函数,
上是增函数, 取
取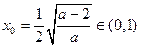 ,则
,则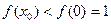 ;
;③当
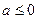 时,对任意
时,对任意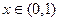 ,恒有
,恒有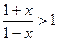 且
且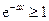 , 得
, 得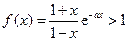 .
.综上,当且仅当
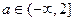 时,若对任意
时,若对任意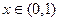 恒有
恒有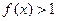 成立.
成立.略

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
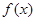 在
在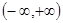 内可导,且
内可导,且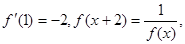 则
则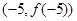 处切线的斜率为( )
处切线的斜率为( )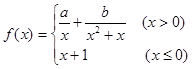 在
在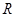 上连续,则
上连续,则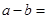 ( )
( )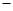 1
1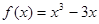 ,若过点A(0,16)的直线方程为
,若过点A(0,16)的直线方程为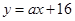 ,与曲线
,与曲线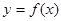 相切,则实数
相切,则实数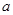 的值是( )
的值是( )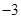
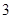
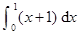 的值为
的值为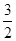
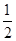
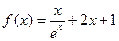 在点
在点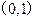 处的切线方程是
处的切线方程是  在点
在点 处的切线方程是
处的切线方程是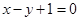 ,则( )
,则( )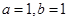
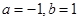
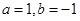
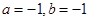
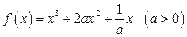 ,则
,则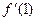 的最小值为
的最小值为  (2)=
(2)=